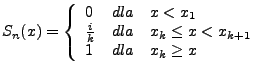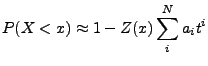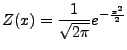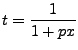Następny: Spis Literatury
W góre: Wybrane Zagadnienia Matematyki II Zadania do zaprogramowania
Poprzedni: Zadanie 4 - Macierz kowariancji (wsp. korelacji)
Subsections
Program powinien obliczać wartość statystyki Kołmogorowa pozwalając sprawdzić hipotezę:
- dane pochodzą z rozkładu normalnego (test poprawności działania
generatora z zadania 3)
- dane pochodzą z rozkładu jednostajnego (test poprawności działania
generatora z zadania 1)
Program powinien wczytać dane tekstowe i wyświetlić wartość statystyki Kołmogorowa (lub
asymptotycznej wartości statystyki Kołmogorowa gdy pomiarów jest więcej niż 100).
Podczas badania normalności rozkładu należy do obliczenia dystrybuanty
zastosować przybliżenie przedstawione
poniżej.
Stawiamy hipotezę
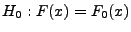 , gdzie
, gdzie 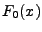 jest dystrybuantą typu
ciągłego (W. Krysicki).
jest dystrybuantą typu
ciągłego (W. Krysicki).
Statystyka testowa:
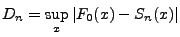 |
(6) |
gdzie 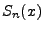 jest dystrybuantą empiryczną ustaloną po posortowaniu próbki
jest dystrybuantą empiryczną ustaloną po posortowaniu próbki
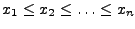 w następujący sposób:
w następujący sposób:
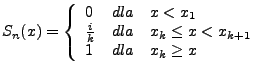 |
(7) |
Przy danym poziomie istotności 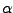 i liczebności
i liczebności 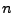 możemy z tablic
statystycznych odczytać krytyczna wartość
możemy z tablic
statystycznych odczytać krytyczna wartość
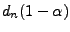 statystyki Kołmogorowa
statystyki Kołmogorowa
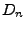 .
.
Obszarem krytycznym jest przedział
![$ [d_n(1-\alpha),1]$](img39.png)
Przy danej liczebności próbki (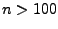 ) można posługiwać się rozkładem granicznym
statystyki
) można posługiwać się rozkładem granicznym
statystyki 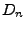 :
:
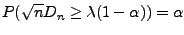 |
(8) |
Najważniejsze wartości kwantyli
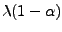 przy rozkładzie granicznym
przy rozkładzie granicznym
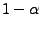
|
0.90 |
0.95 |
0.99 |
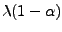
|
1.224 |
1.354 |
1.628 |
Jeżeli więc obliczona wartość
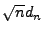 jest większa od krytycznej wartości
(kwantyla)
jest większa od krytycznej wartości
(kwantyla)
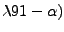 , to hipotezę na poziomie istotności
, to hipotezę na poziomie istotności 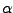 odrzucamy.
odrzucamy.
Przybliżona wartość dystrybuanty rozkładu
normalnego
Jedną z metod wyznaczania przybliżonej wartości dystrybuanty
rozkładu normalnego jest rozwinięcie w szereg postaci (Abramowitz and
Stegun)
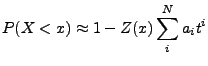 |
(9) |
gdzie
dla N=5 odpowiednie stałe wynoszą:
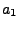
|
0.319381530 |
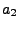
|
-0.356563782 |
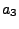
|
1.781477937 |
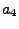
|
-1.821255978 |
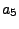
|
1.330274429 |
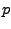
|
0.2316419 |
Dokładność przybliżenia :
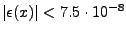
Przykładowa implementacja w języku C



Następny: Spis Literatury
W góre: Wybrane Zagadnienia Matematyki II Zadania do zaprogramowania
Poprzedni: Zadanie 4 - Macierz kowariancji (wsp. korelacji)
2006-05-22