


Następny: Zadanie 2 - Statystyki opisowe
W góre: Wybrane Zagadnienia Matematyki II Zadania do zaprogramowania
Poprzedni: Wybrane Zagadnienia Matematyki II Zadania do zaprogramowania
Subsections
Zadanie 1 - Generator liczb z rozkładu jednostajnego
Program generujący zadaną liczbę wartości pochodzących z rozkładu jednostajnego na
odcinku [0,1] przy wykorzystaniu:
- algorytmu MLCG
- funkcji random dostępnej w danym języku programowania
Jeżeli nie jest to aplikacja konsolowa to program powinien
posiadać możliwość zapisania wygenerowanych liczb do pliku tekstowego.
Generator oparty jest na zasadzie iteracyjnej:
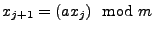 |
(1) |
gdzie wszystkie wartości są liczbami całkowitymi. Wartość początkowa 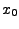 (seed) jest dowolną liczbą całkowitą z zakresu obejmującego okres generatora.
(seed) jest dowolną liczbą całkowitą z zakresu obejmującego okres generatora.
Algorytm (przenośny) Wichmanna, Hilla oraz L'Ecuaya: zakładamy, że mnożnik 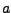 spełnia warunek
spełnia warunek 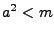 .
.
Definiujemy
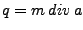 |
(2) |
oraz
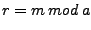 |
(3) |
tak aby 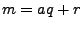 , wówczas po przekształceniach
otrzymujemy:
, wówczas po przekształceniach
otrzymujemy:
![$\displaystyle [ax] \:mod \: m=\left[a(x \: mod\: q) - (x \: div\: q )r\right]\mod{m}$](img8.png) |
(4) |
gdzie wyrażenie w nawiasie zawiera się w przedziale ![$ [-m,m]$](img9.png) dla
dla 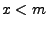 .
.
Stąd kolejne losowe liczby całkowite 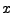 możemy wygenerować za pomocą algorytmu:
możemy wygenerować za pomocą algorytmu:
k = x / q
x = a * ( x - k * q ) - k * r
if ( x < 0 ) then x = x + m
Wartości mnożnika 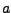 oraz modułu
oraz modułu 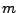 muszą spełniać odpowiednie warunki aby zagwarantować dostatecznie długi okres liczb losowych.
muszą spełniać odpowiednie warunki aby zagwarantować dostatecznie długi okres liczb losowych.
Wartości 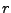 i
i 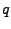 są stałymi obliczonymi według wzorów (2,3).
są stałymi obliczonymi według wzorów (2,3).
W poniższej tabeli zawartych jest kilka właściwych wartości dla maszyny 32 bitowej (S. Brandt):
| m |
a |
| 2147483647 |
39373 |
| 2147483563 |
40014 |
| 2147483399 |
40692 |
Okres całego szeregu wynosi 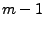 , algorytm jest przenośny gdyż wszystkie obliczenie są dokonywane w arytmetyce liczb całkowitych.
, algorytm jest przenośny gdyż wszystkie obliczenie są dokonywane w arytmetyce liczb całkowitych.
Chcąc otrzymać liczby zmiennopozycyjne z zakresu ![$ [0,1]$](img16.png) należy wynik podzielić przez
należy wynik podzielić przez 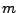 .
.



Następny: Zadanie 2 - Statystyki opisowe
W góre: Wybrane Zagadnienia Matematyki II Zadania do zaprogramowania
Poprzedni: Wybrane Zagadnienia Matematyki II Zadania do zaprogramowania
2006-05-22