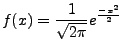Następny: Zadanie 4 - Macierz kowariancji (wsp. korelacji) W góre: Wybrane Zagadnienia Matematyki II Zadania do zaprogramowania Poprzedni: Zadanie 2 - Statystyki opisowe

Subsections

• Metoda biegunowa Boxa i Mullera

Zadanie 3 - Generowanie liczb z rozkładu normalnego

Program generujący zadaną liczbę wartości pochodzących z rozkładu 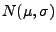$N(\mu,\sigma)$ przy wykorzystaniu algorytmu Boxa i Mullera.
Jeżeli nie jest to aplikacja konsolowa to program powinien posiadać możliwość zapisania wygenerowanych liczb do pliku tekstowego.

Metoda biegunowa Boxa i Mullera

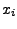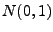
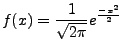Chcemy wygenerować liczby losowe $x_i$ posiadające rozkład normalny $N(0,1)$

$$f(x)=\frac{1}{\sqrt{2\pi}}e^\frac{-x^2}{2}$$ (5)

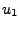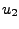1. generujemy dwie niezależne liczby losowe $u_1$ i $u_2$ , zgodnie z rozkładem jednostajnym na odcinku $[0,1]$ (patrz zadanie 1)
2. dokonujemy transformacji $v_1=2u_1-1$ , $v_2=2u_2-1$
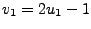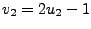
3. obliczamy $s=v_1^2+v_2^2$
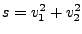
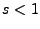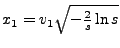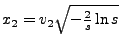4. jeśli $s<1$ to liczby $x_1=v_1\sqrt{-\frac{2}{s}\ln{s}}$ oraz $x_2=v_2\sqrt{-\frac{2}{s}\ln{s}}$ są dwiema niezależnymi liczbami losowymi mającymi standardowy rozkład normalny