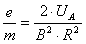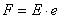
Wyznaczanie
ładunku właściwego e/m za pomocą lampy elektronowej
Thomsona
Analiza
ruchu
elektronu
w
polu
elektrycznym i magnetycznym:
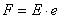
W polu elektrycznym jest to jedyna siła. która oddziałuje na elektron (w porównaniu z siłą elektryczną pomijane są siły grawitacji i siły wzajemnych oddziaływań między elektronami), Zgodnie z drugą zasadą dynamiki Newtona siłę można wyrazić jako:
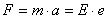
gdzie: m - masą elektronu;
a - przyspieszeniem elektronu.
W związku z tym, że elektron w polu elektrycznym porusza się
ruchem jednostajnie przyspieszonym, to przyspieszenie elektronu w
kierunku
odchylenia (kierunek w poprzek
płytek), wynosi:
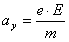
Droga w takim ruchu wyraża się zależnością:
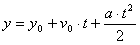
gdzie: oraz
oraz  .
Zatem:
.
Zatem:
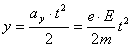 (1)
(1)
W kierunku x (kierunek wzdłuż płytek)
nie działa żadna siła, więc elektrony poruszają się ruchem jednostajnym:
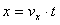 (2)
(2)
Wyznaczenie parabolicznej trajektorii elektronu jest możliwe, gdy do równania (2) wstawi się równanie (1):
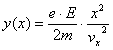 (3)
(3) Parametrów e/m oraz 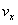 nie da się w sposób
bezpośredni wyznaczyć. Aby to jednak uczynić Thomson zrównoważył siłę
elektryczną siłą Lorentza, poprzez umieszczenie lampy w zewnętrznym i jednorodnym
polu magnetycznym. Na elektron o ładunku e w jednorodnym polu
magnetycznym o indukcji B,
który
porusza
się
z
prędkością ,
działa
siła Lorentza F prostopadła do prędkości
i indukcji pola:
nie da się w sposób
bezpośredni wyznaczyć. Aby to jednak uczynić Thomson zrównoważył siłę
elektryczną siłą Lorentza, poprzez umieszczenie lampy w zewnętrznym i jednorodnym
polu magnetycznym. Na elektron o ładunku e w jednorodnym polu
magnetycznym o indukcji B,
który
porusza
się
z
prędkością ,
działa
siła Lorentza F prostopadła do prędkości
i indukcji pola:
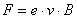
Jeśli pole magnetyczne jest prostopadłe do pola elektrycznego, to
można tak dobrać wartości pól, aby siły się równoważyły. Jeżeli siły
będą się
równoważyły, to tor elektronu nie ulegnie odchyleniu (zerowe ugięcie):
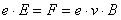
Prędkość w kierunku osi x będzie więc równa:
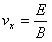 (4)
(4)
Zmodyfikowane równanie parabolicznej trajektorii elektronu otrzyma się wstawiając równanie (4) do równania (3):
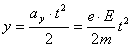
Analiza
ruchu
elektronu
w
poprzecznym
polu magnetycznym:
Elektrony poruszając się z punktu o potencjale 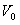 do punktu o
potencjale
do punktu o
potencjale
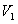 , zmieniają zarówno swoją energię kinetyczną jak i
potencjalną:
, zmieniają zarówno swoją energię kinetyczną jak i
potencjalną:
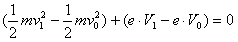
Różnica potencjałów w danych punktach jest napięciem anodowym
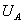 , natomiast początkowa prędkość elektronów jest równa
, natomiast początkowa prędkość elektronów jest równa 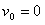 . Zatem:
. Zatem:
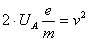 (5)
(5)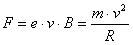
gdzie: R - promień krzywizny toru elektronów (stały).
Stąd:
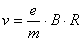 (6)
(6)
Korzystając ze wzoru (5) i (6) otrzyma się stosunek e/m równy: