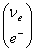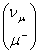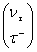Unifikacja oddziaływań słabych i elektromagnetycznych

           
Unifikacja oddziaływań słabych i elektromagnetycznych nastąpiła na początku lat   60-tych ubiegłego wieku. Istniało kilka przesłanek, wskazujących na możliwość takiej unifikacji. Przesłanki te oparte były na pewnych własnościach symetrii. Ich szczegółowa analiza wykracza poza zakres tej pracy. Niektóre konstrukcje formalne wykorzystywane w budowie modelu oddziaływań elektromagnetyczno-słabych (nazywanych w skrócie oddziaływaniami elektro-słabymi) opisane są w dalszej części tego podrozdziału.

W każdej generacji leptonów mamy dwie cząstki. Można opisać każdą rodzinę leptonową, jako jedną całość, za pomocą trzech macierzy o dwu elementach:

, , .

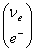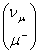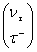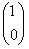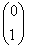Górny wiersz opisuje prawdopodobieństwo istnienia jako neutrino elektronowe (mionowe lub taonowe), natomiast dolny opisuje prawdopodobieństwo istnienia jako elektron (mion lub taon). Zatem neutrino  i antyneutrino opisane są odpowiednio:i (1  0). Elektron (mion lub taon) opisane jest przez macierz , zaś ich antycząstki opisane są przez macierz (0  1). Bozony oddziaływania słabego są reprezentowane przez następujące macierze o wymiarach 2×2:

 ,

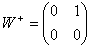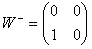
Zderzenie tych bozonów można przedstawić jako:

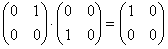
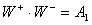
lub

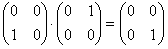
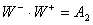
W ten sposób powstały dwie nowe macierze 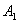 i 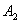, które można by interpretować jako sugestię istnienia jakiejś nowej cząstki, która jest partnerem bozonów W, ale nie ma ładunku elektrycznego. Badając jej oddziaływanie z neutrinem można stwierdzić, że cząstką tą nie jest foton. Fotony bowiem nie oddziałują z pozbawionymi ładunku elektrycznego neutrinami. Rachunek macierzowy natomiast pokazuje, że nowa cząstka oddziałuje z neutrinem. Cząstką tą będzie więc trzeci, neutralny bozon oddziaływań słabych, który oznaczono .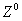

W 1961 roku Sheldon Glashow uzyskał pierwszy działający model, który jednoczył oddziaływanie słabe i elektromagnetyczne, za co w 1979 roku został uhonorowany nagrodą Nobla (wspólnie z A. Salamem i S. Weinbergiem). Macierzową teorią oddziaływań słabych nazywamy teorią SU(2) (zbiór tych macierzy tworzy grupę SU(2)). Tworzą ją macierze 2×2, które mają tę własność, że suma elementów leżących na przekątnej macierzy (od lewego górnego do prawego dolnego rogu) jest równa zeru. Teoria ta dopuszcza macierze:

,      ,    

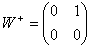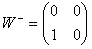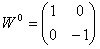
gdzie: W⁰ jest różnicą macierzy 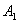 oraz .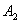

Macierzową teorię oddziaływań elektromagnetycznych nazywamy teorią U(1). Jej konstrukcja wykorzystuje symetrię odpowiedzialną za istnienie prawa zachowania ładunku elektrycznego. W języku macierzowym oparta jest na macierzy 1×1 (stąd nazwa U(1)).

Jednoczesne uwzględnienie słabego i elektromagnetycznego oddziaływania prowadzi do teorii SU(2)·U(1). W teorii tej do cząstek 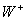, 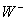 i 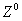 dochodzi czwarta cząstka, która związana jest z członem U(1). Jest to elektrycznie obojętny bozon:

Ostatecznie unifikacja oddziaływań elektro-słabych daje cztery nośniki tych oddziaływań, czyli:

,     ,   ,

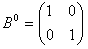
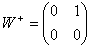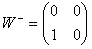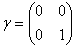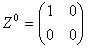
W tej teorii foton jest kwantową superpozycją cząstek W⁰ oraz B⁰. Cząstki W⁺ i W^- przenoszą ładunkowe oddziaływanie słabe (przenoszą ładunek elektryczny), natomiast Z⁰ przenosi neutralne oddziaływanie słabe i podobnie jak foton jest superpozycją cząstek W⁰ oraz B⁰ .