Analiza harmoniczna

Rozkład funkcji (sygnału) na sumę składowych harmonicznych postaci   

sin nx   i   cos nx

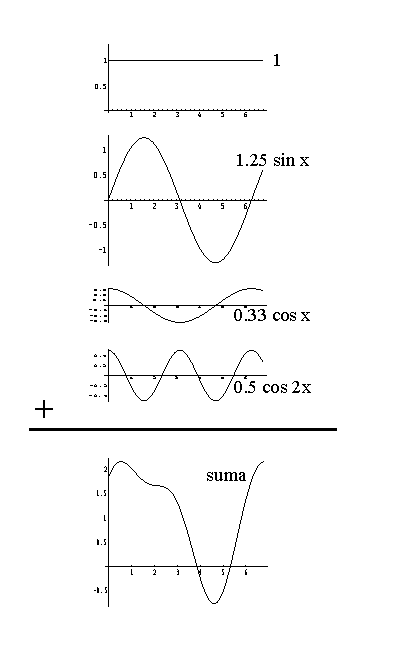
Przykład: Funkcja f(x) jest sumą prostych funkcji trygonometrycznych

f(x)  =  1  +  1.25 sin x  +  0.33 cos x  +  0.5 cos 2x 

Pełną informację o tej funkcji można zakodować za pomocą kilku liczb przyjmując konwencję, że kolejne dane oznaczają współczynniki (amplitudy) stojące przy odpowiednich składowych trygonometrycznych:

Odwrotnie: mając dany wykres pewnej funkcji g(x), np.

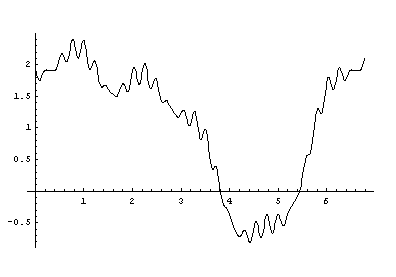
można się zastanawiać jak (w sposób możliwie dokładny) przedstawić ją jako sumę składowych harmonicznych, a tym samym jak zakodować ją za pomocą ciągu amplitud. W tym przykładzie

g(x)   =   1  +  1.25 sin x  +  0.33 cos x  +  0.5 cos 2x  
-  0.2 sin 5x  +  0.1 cos 25x  -  0.07 sin 30x

czyli g(x) można zakodować jako ciąg amplitud

1  1.25  0.33  0  0.5  0 ... 0  -0.2  0 ... 0  0.1  0 ... 0  -0.07

Algorytm wyliczania ciągu amplitud dla zadanej funkcji nosi nazwę 
transformacji Fouriera.

Ciąg amplitud wygodnie jest uważać za funkcję zmiennej n, oznaczając ją przez g^(n) - nosi ona nazwę  transformaty Fouriera  dla g(x).

W pewnym uproszczeniu, składowe harmoniczne wysokiej częstotliwości są odpowiedzialne za "szczegóły" na wykresie g(x), natomiast niższe częstotliwości zawierają w sobie przybliżony "zarys" przebiegu g(x). 

Np. usuwając powyższym przykładzie składniki  0.1 cos 25x  i  
-0.07 sin 30x  dostaniemy

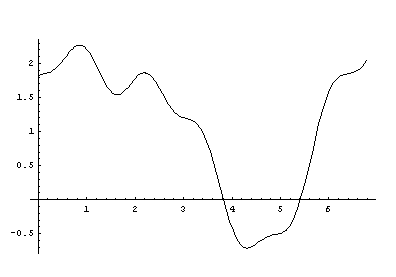
g(x)  ≈  1  +  1.25 sin x  +  0.33 cos x  +  0.5 cos 2x  -  0.2 sin 5x 

Manipulacje na transformatach Fouriera, polegające na usuwaniu wyższych częstotliwości można zastosować na 2 sposoby:
- do "wygładzania" funkcji;
- do "kompresji" danych.