Zadanie 3

Kometa Halleya obiega Słońce po wydłużonej elipsie ( e = 0,9673 ). Okres obiegu komety wokół Słońca  jest równy 75, 98 lat. Oblicz odległość komety Halleya od Słońca, gdy znajduje się w peryhelium i aphelium.

Rozwiązanie:
Z III prawa Keplera wynika, że stosunek  (gdzie: T – okres obiegu danego ciała wokół innego, a – średnia odległość obu tych ciał od siebie) jest stały dla wszystkich

orbit ciał krążących wokół tego samego ciała o dużej masie. Zatem:

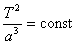
Aby związek ten posłużył do wyznaczenia średniej odległości komety Halleya od Słońca należy wziąć pod uwagę ciało, którego charakterystykę dobrze znamy. Wtedy z równania:

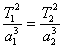
z łatwością wyznaczyć będzie można średnią odległość komety od Słońca:

Wiadome jest, że Ziemia obiega Słońce w ciągu 1 roku i znajduje się w odległości 1 jednostki astronomicznej (1 j.a. = 149597870691 ± 30 m) od niego. Zatem:

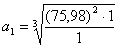
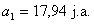
Korzystamy teraz  z równania biegunowości elipsy:

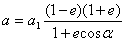
gdzie: e – mimośród elipsy

Dla peryhelium i aphelium mamy odpowiednio kąt alfa równy 0° oraz 180°, więc otrzymamy dwa równania:

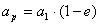
Zatem:

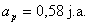
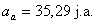
Odpowiedź: Odległość komety od Słońca wynosi 0,58 j.a., gdy znajduje się ona w peryhelium oraz 35,29 j.a., gdy znajduje się ona w aphelium.