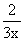Zadanie 2

Traktor w ciągu 2 godzin zaorał 1/3 część pola, po nim pracował drugi traktor, który zaorał pole do końca. Gdyby oba traktory pracowały jednocześnie, to zaorałyby pole w ciągu liczby godzin będącej średnią arytmetyczną liczby godzin, które zużyłby każdy z nich, wykonując swoją część pracy samodzielnie. Ile godzin orał drugi traktor?

Rozwiązanie:

Dane:

t’₁ = 2 h

t’₂ = x h

Szukane:

t – całkowity czas pracy obu traktorów pracujących jednocześnie

Pierwszy traktor pracował 2 godziny i zaorał 1/3 pola. Drugi traktor pracował x godzin i zaorał 2/3 pola. Zatem w ciągu jednej godziny pierwszy traktor zaorałby 1/6 pola, a drugi zaorałby 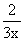 pola .

Pierwszy traktor orałby więc całe pole przez 6 godzin, a drugi całe pole zaorałby w czasie 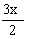 godzin. Otrzymujemy więc dwie kolejne dane postaci:

t₁ = 6 h

t₂ = 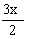 h

Wydajność pracy pierwszego i drugiego traktora przedstawić można więc równaniem:

Wiemy również, że czas jaki musiałyby poświęcić oba traktory pracując jednocześnie, aby zorać całe pole jest średnią arytmetyczną liczby godzin, które zużyłby każdy z nich, wykonując swoją część pracy samodzielnie. Zatem:

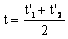
Podstawiając drugie równanie do pierwszego otrzymamy:

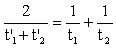
Wstawiając dane do równania mamy:

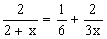
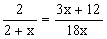
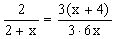
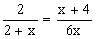
Mnożąc równanie na krzyż otrzymujemy:

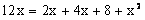
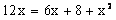
Otrzymaliśmy więc równanie kwadratowe. Aby je rozwiązać należy policzyć deltę i pierwiastki.

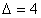
Obliczamy teraz pierwiastki równania, czyli jego rozwiązania:

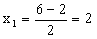
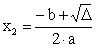
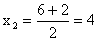
Odpowiedź:  Pracując jednocześnie traktory zaorałyby pole w ciągu 2 lub 4 godzin.