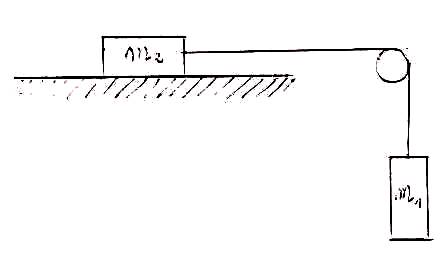
Zadanie 1

Jakie jest przyspieszenie a masy m₂ w zaprezentowanej sytuacji:

wiedząc, że m₁ = 250g oraz m₂ = 500g? Jak zmieni się przyspieszenie, gdy do masy m₁ dodamy klocek o tej samej masie? Tarcie pomijamy.

Rozwiązanie pierwszej części zadania:

Z zadania wynika, że masa m₂ jest dwa razy większa od masy m₁. Zatem możemy zapisać, że:

m₂ = 2 · m₁

I sposób

Przyspieszenie zgodnie z II zasadą dynamiki Newtona jest wprost proporcjonalne do działającej na ciało siły i odwrotnie proporcjonalne do masy ciała, na które działa ta siła:

a = F/m

Nasz układ złożony jest z dwóch ciał (klocków o masach m₁ i m₂). Aby wyznaczyć przyspieszenie a trzeba więc znaleźć stosunek siły wypadkowej działającej na ten układ i całkowitej masy tego układu. Wtedy przyspieszenie będziemy mogli policzyć ze wzoru:

a = F_wyp / (m₁ + m₂)

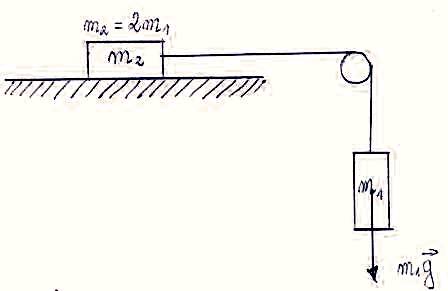
Wypadkową siłą  jest siła grawitacyjna działająca na klocek o masie m₁.

Zatem

a = m₁g / (m₁ + 2m₁) = m₁g / 3m₁ = 1/3 g

Odpowiedź:  Przyspieszenie a jest równe 1/3 przyspieszenie ziemskiego (grawitacyjnego).

II sposób

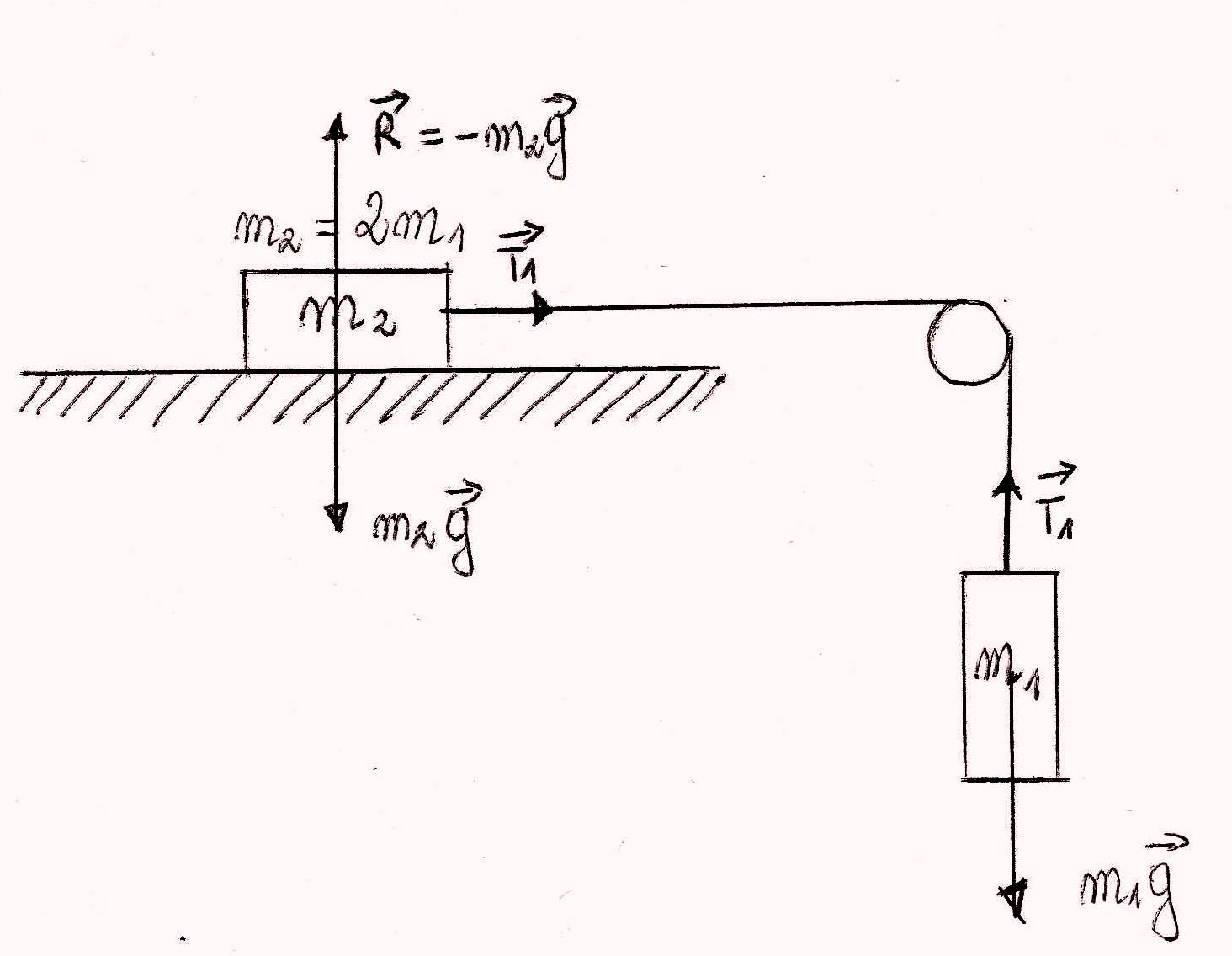
Zakładamy, że w danym układzie nić łącząca m₁ oraz m₂ jest wiotka, cienka i nierozciągliwa, a masa kołowrotka jest porównywalnie mała z m₁ oraz m₂. Założenie to dużo nam mówi o sytuacji, z jaka mamy do czynienia w zadaniu. Fakt, że nić jest cienka mówi o tym, że jej masę możemy pominąć w rozwiązywaniu zadania, natomiast to że jest wiotka, znaczy tyle, że siły przenoszone są stycznie miedzy klockami.

Na ciała m₂ działa zatem siła naciągu nici T₁ skierowana wzdłuż nici w kierunku klocka m₁. Siła naciągu nici jest równa:

T₁ = m₂ · a = 2m₁ · a

Na klocek m₁ również działa siła naciągu nici T₁ skierowana pionowo przeciwnie do działającej siły grawitacyjnej.

Przyspieszenie a₂ dla klocka o masie m₂ wynosi:

a₂ = T₁ / 2m₁

Przyspieszenie a₁ dla klocka o masie m₁ wynosi:

a₁ = (m₁g – T₁) / m₁ = g – (T₁ / m₁)

Przyspieszenie to jest inne, gdyż na klocek o masie m₁ działa dodatkowo siła grawitacyjna.

W związku z tym, że nić jest nierozciągliwa, to przyspieszenia a₁ oraz a₂ są równe. Zatem

a₁ = a₂

T₁ / 2m₁ = g – (T₁ / m₁)

T₁ = 2m₁g – 2T₁

3T₁ = 2m₁g

Ale wiemy, że T₁ = 2m₁a, więc

3· 2m₁a = 2m₁g

3a = g

a = 1/3 g

Odpowiedź:  Przyspieszenie a jest równe 1/3 przyspieszenie ziemskiego (grawitacyjnego).

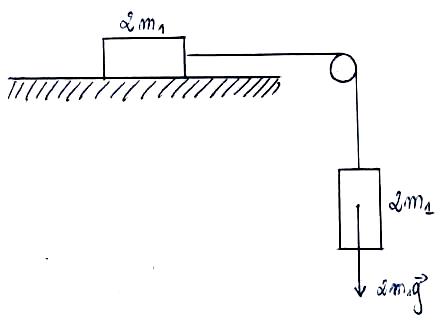
Rozwiązanie drugiej części zadania:

Jeżeli do masy m₁ dodamy dodatkowe obciążenie o tej samej masie, to będziemy mieć sytuację, w której masa m₁ będzie równa 2m₁ oraz masa m₁ będzie równa 2m₁.

Zatem rozwiązanie zadania jest analogiczne do części pierwszej:

Wiemy, że przyspieszenie jest wprost proporcjonalne do działającej na ciało siły i odwrotnie proporcjonalne do masy ciała, na które działa ta siła. Można więc zapisać to jako:

a = F/m

Nasz układ złożony jest z dwóch ciał (klocków o masach m₁ i m₂). Aby wyznaczyć przyspieszenie a trzeba więc znaleźć stosunek siły wypadkowej działającej na ten układ i całkowitej masy tego układu. Wtedy przyspieszenie będziemy mogli policzyć ze wzoru:

a = F_wyp / (m₁ + m₂)

Wypadkową siłą  jest siła grawitacyjna działająca na klocek o masie m₁.

Zatem

a = 2m₁g / (2m₁ + 2m₁) = 2m₁g / 4m₁ = 1/2 g