Understanding the data

Neural methods of knowledge extraction

The trouble with doing something right the first time
is that nobody appreciates how difficult it was.

Anonymous

Review and comparison of many rule extraction methods:

R. Andrews, J. Diederich, A.B. Tickle, "A Survey and Critique of Techniques for Extracting Rules from Trained Artificial Neural Networks," Knowledge-Based Systems vol. 8, pp. 373-389, 1995.

Neural rule extraction algorithms differ in:

1. the "expressive power" of the extracted rules (types of rules extracted);
2. the "quality" of the extracted rules (accuracy, fidelity comparing to the underlying network, comprehensibility and consistency of the extracted rules);
3. the "translucency" of the method - analysis of individual nodes versus analysis of the total network function;
4. the algorithmic complexity of the method;
5. specialized network training schemes;
6. the treatment of linguistic variables.

Early papers:

K. Saito, R. Nakano, "Medical diagnostic expert system based on PDP model", Proc. of IEEE Int. Conf. on Neural Networks (San Diego CA), Vol 1 (1988) 255-262
Restrictions on the form of rules, the maximum number of positive and negative conditions, the depth of the breadth-first search process, including only conditions that were present in the training set.

KT algorithm: L.M. Fu, "Neural networks in computer intelligence", McGraw Hill, New York, 1994
Local method, conjunctive rules, depth of search is restricted. Network weights help to limit the search tree.

SUBSET algorithm

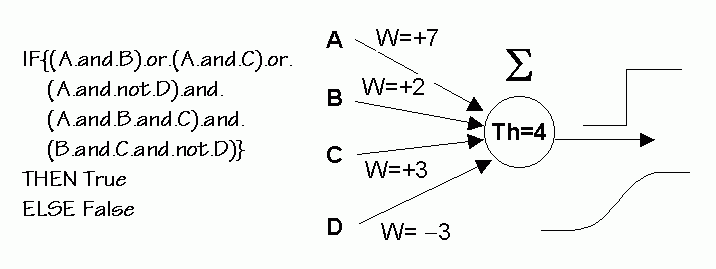
G. Towell, J. Shavlik, "Extracting refined rules from knowledge-based neural networks". Machine Learning 13 (1993) 71-101

Analyze incoming weights of hidden and output neurons.
Consider all possible subsets of incoming weights W_i, positive or negative.
Find all combinations > Th

Example:

Problem: number of subsets is 2^Ninp.
Exponentially growing number of possible conjunctive propositional rules.
Partial solution: restrict the number of antecedents, subsets or rules using some heuristics.
inputs with largest weights are analyzed first, combinations of two largest weights follow, until the maximum number of antecedent conditions is reached.

RuleNet

C. McMillan, M.C. Mozer, P. Smolensky, "Rule induction through integrated symbolic and subsymbolic processing". In: J. Moody, S. Hanson, R. Lippmann, eds, Advances in NIPS 4, Morgan Kaufmann, San Mateo, CA 1992
J.A. Alexander, M.C. Mozer, "Template-based algorithms for connectionist rule extraction". In: G. Tesauro, D. Touretzky, T. Leen, eds, Advances in NIPS 7, MIT Press, Cambridge, MA, 1995

Used to find M of N rules and propositional rules.
Make hypothesis and test them - training algorithm, called “The Connectionist Science Game”, consists of 3-steps:

1. Train RuleNet network.
2. Extract symbolic rules using weight analysis.
3. Inject rules back into the network.

RulNet: 3 layer network, input, condition units and output action units.
Use weight templates exploring large spaces of candidate rules.
Only discrete-valued features, specific architecture for string-to-string mapping, for example character strings, not a general technique.

M-of-N method

G. Towell, J. Shavlik, "Extracting refined rules from knowledge-based neural networks". Machine Learning 13 (1993) 71-101

Rules of the form:
IF M of N antecedents are true THAN ....
Sometimes more compact and comprehensible than conjunctive rules.

Used in KBANN (Knowledge-Based ANN) networks, where symbolic knowledge is used to specify initial weights.

1. For each hidden and output unit form groups of similarly-weighted links.
2. Set all link weights to average of the group.
3. Eliminate groups that do not affect the output.
4. Use prototype weight templates (corresponding to symbolic rules) for comparison with the weight vectors.
5. Freeze weights, reoptimize biases.
6. Form single rule for each hidden and output unit.

IF(M of N antecedents (A₁, A₂ ... A_N ) are true) THEN ...

Newer work: M of N3 algorithm:
R. Setiono, "Extracting M of N Rules from Trained Neural Networks", Transactions on Neural Networks 11 (2000) 512-519
Penalty term to prune the network, inputs should be binary.

REAL (Rule Extraction As Learning)

M. W. Craven, J.W. Shavlik, "Using sampling and queries to extract rules from trained neural networks". In: Proc. of the Eleventh Int. Conference on Machine Learning, New Brunswick, NJ. Morgan Kaufmann 1994, pp. 37-45

Rule extraction = learning logical function that approximates the target (neural network) function.

• Get new example,
• use existing rules to classify it,
• if wrong add a new rule based on this example,
• check if the extended set of rules still agree with NN.

Rules: IF ... THEN ... ELSE, M-of-N

VIA (Validity Interval Analysis)

S. Thrun, "Extracting rules from artifcial neural networks with distributed representations". In: G. Tesauro, D. Touretzky, T. Leen, eds, Advances in Neural Information Processing Systems 7. MIT Press, Cambridge, MA, 1995

Extract rules mapping inputs directly to the outputs, try to capture what does the network do, global method.

1. Assign arbitrary “validity intervals” to all NN units
   Restrictions on the input/activation values of units.
2. Refine the intervals by changing those that are never activated.
3. Analyze the intervals and derive rules.

Rules: IF ... THEN ... ELSE
Numerous rules, too specific. Has not been used much?

RULENEG

E. Pop, R. Hayward, J. Diederich, "RULENEG: extracting rules from a trained ANN by stepwise negation", QUT NRC technical report, December 1994;
R. Hayward, C. Ho-Stuart, J. Diederich and E. Pop, "RULENEG: extracting rules from a trained ANN by stepwise negation", QUT NRC technical report, January 1996

Forms conjunctive rules, one per input pattern.

For input pattern that is not correctly classified by the existing set of rules:

For i =1..N
Determine class of (x₁, ... NOT.x_i, ... x_N)
If the class has changed add R = R.AND.x_i

BRAINNE

S. Sestito, T. Dillon, "Automated knowledge acquisition". Prentice Hall (Australia), 1994

Network of M inputs and N outputs is changed to a network of M+N inputs and N outputs and retrained.

Original inputs that have weights which change little correspond to the most important features.

DEDEC

A.B. Tickle, M. Orlowski, J. Diederich, "DEDEC: decision detection by rule extraction from neural networks", QUT NRC technical report, September 1994

Rule extraction: find minimal information distinguishing a given pattern from others from the NN point of view.

Rank the inputs in order of importance - determine the importance of input features, using input weights.
Select clusters of cases with important features (using k-NN ) and use only those features to derive rules.
Learn rules using symbolic induction algorithm.

RULEX

R. Andrews, S. Geva, "Rule extraction from a constrained error back propagation MLP". Proc. 5th Australian Conference on Neural Networks, Brisbane, Queensland 1994, pp. 9-12

Special MLP network, using local response units - combination of sigmoids in one dimension, forming ridges.

Disjoint regions of the data <--> one hidden unit.

Similar to symmetric trapezoid neurofuzzy approach.

Trained with Constrained Backpropagation (some weights are kept fixed).
Inserting and refining rules is possible.

Propositional Rules:

IF Ridge₁ is active and Ridge₂ is active and .... THEN Class_k

Works for continuos & discrete inputs.

TREPAN

M. W. Craven, J.W. Shavlik, "Extracting tree-structured representations of trained networks". In: D. Touretzky, M. Mozer, M. Hasselmo, eds, Advances in NIPS 8, MIT Press, Cambridge, MA 1996.

Decision tree instead of rules - inductive algorithm.

NN treated as “oracle” answering queries.
Queries may be incomplete patterns.
Oracle determines class labels, is used to selects splits of nodes and to check if a tree node covers a single class only.

Tree expansion: best-first method, with node splits representing binary and M-of-N rules.
Spilt: partition input space to increase separation of input patterns into classes.
Nodes evaluated by: % cases reaching it times the % of errors in the node.
Split selected only after >1000 cases considered.
Thanks to oracle - works better than other inductive algorithms.

Conclusion: if a black box classifier works well on your data and rule-based description is required - use it as oracle!

Successive Regularization

M. Ishikawa, "Rule extraction by succesive regularization". In: Proc. of 1996 IEEE Int. Conf. on Neural Networks. Washington, 1996, pp. 1139-1143.

Structural learning with forgetting (SLF):

MLP with Laplace-type regularizing term:

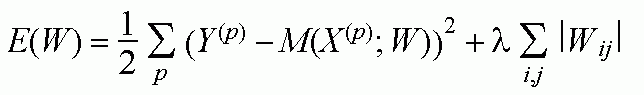
(X^(p), Y^(p)) - question-response patterns p;
W_ij - connection weight between units i and j.

Selective forgetting: only weights smaller than some threshold are included in the regularizing term.
This term leads to a constant decay of smaller weights.
Small weights are pruned and a skeletal network emerges.

Clarification of hidden units: 0/1 outputs forced by penalty term
c S_i min (1-h_i,h_i)

Successive regularization:
Start from rather large l, get dominant rules first.
Fix the parameters of this part of the network.
Decrease l, train network => more connections left, more rules.

Skeletal structure + 0/1 outputs of hidden units => each node is represented as a logical function of nodes in the adjacent lower layer.
Good method but requires many experiments to find good initial network.

Other methods

• P. Geczy and S. Usui, "Rule extraction from trained neural networks". Int. Conf. on Neural Information Processing, New Zealand, Nov.1997, Vol. 2, pp. 835-838

  Train the network.
  Replace resulting weights by resulting 0, +1 and -1
  Extract logical functions performed by the network.

• H. Tsukimoto, "Extracting Rules from Trained Neural Networks" , Transactions on Neural Networks 11 (2000) 377-389

  Approximation of MLPs by by Boole'an functions.
  Network function is approximated by lower order logical polynomials.
  Results are not too good.

• R. Setiono and H. Liu, "Neurolinear: From neural networks to oblique decision rules". Neurocomputing (in print).
  Oblique decision rules, linear combination of inputs.

• R. Setiono, "Extracting rules from neural networks by pruning and hidden-unit splitting". Neural Computation, Vol. 9, No. 1, pp. 205-225.
  Prune the network to get small number of inputs connected to a hidden unit.
  Split the hidden node treating it as a few output units, each activation as a target value.
  Add new hidden layer, train and prune.
  Few results so far.

Decision-tree based methods of rule extraction

General remarks:
Decision Trees (DT) are simple to use, use a few parameters, provide simple rules.

Most DT are univariate, axis-parallel.
Oblique trees use linear combinations of input features.

D - training set partitioned into D_k subsets by some tests T.
Stop(D_k)=True if assumed leaf purity is reached.

• If Stop(D) the tree is a leaf associated with the most frequent class in D.
• Test T has mutually exclusive outcomes T_i, i =1...K, subset D_i is composed from cases for which T_i=True.
• Splitting criterion is defined S(T(x)).
• For a discrete attribute test A=?
• A<t for a continuous attribute A;
  if A has values v₁< v₂< ... v_N< check all t = (v_i+ v_i+1)/2;
  select the best S(T(t))

Trees are pruned to improve generalization and to generate simpler rules.

CART, Classification and Regression Tree

Breiman, L., Friedman, J., Olshen, R., and Stone, C. (1984) Classification and Regression Trees", Wadsworth.

Split criterion is based on Gini(node) index:

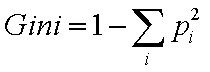
p_i is the probability of class i vectors in the node.

For each possible split calculate Gini, select split with minimum impurity.
Use minimal cost-complexity pruning, rather sophisticated.

DB-CART - added boosting and bagging.
Boosting: making a committee of many classifiers trained on the same training data, with re-weighted wrongly classified cases.
Bagging, bootstrap aggregating: making a committee of many classifiers trained on subsets of data created from the training set by bootstrap sampling (i.e. drawing samples with replacement).

Commercial version of CART and IndCART: different ways of handling missing values and pruning.

C 4.5

Quinlan, J. R. (1993). C4.5: Programs for Machine Learning. San Mateo: Morgan Kaufmann.

C 4.5 splitting criterion is the gain ratio:
for C classes and fraction p(D;j)=p(C_j|D) in j-th class
the number of information bits the set D contains is:

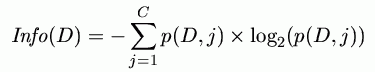
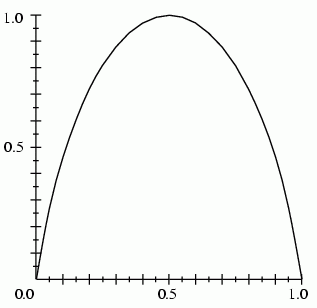
For 2 classes information (vertical) changes with p(D;1)=1-p(D;2) reaching max. for 0.5
Info = expected number of bits required to encode a randomly selected training case.

Information gained by a test T with k possible values is:

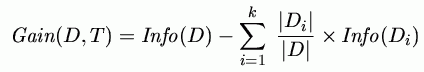
Max. for tests separating D into one-dimensional subsets; attributes with many values are always selected.
Use information gain ratio instead: gain divided by the split information

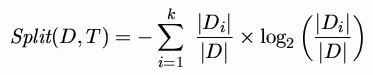
Improvements of continuous attribute treatment in C5:

• The Minimum Description Length (MDL) principle is used: minimize theory and exceptions costs
  Modify Gain(D;T) - log₂ (N-1)/|D|
• Threshold t is chosen to maximize gain.

C4.5 rule generation algorthm, used usually before pruning.
Convert each tree path to a rule:
IF Cond₁ AND Cond₂ ... AND Cond_n THEN class C

• Remove conditions which are not useful.
• Remove empty rules and identical rules.
• Group all rules according to classes.
• Delete rules if the accuracy of the whole set of rules for the class is not lowered.
• Ordered the rules to minimize false positive errors.
• Try to delete rules in turn if accuracy of the whole ruleset on the training set is not lowered.

Z. Zheng, "Scaling Up the Rule Generation of C4.5". Proc. of PAKDD'98, Berlin: Springer Verlag, 348-359, 1998.

Rules are frequently more accurate and simpler than trees, especially if generated from pruned trees.

ANN-DT - Decision Trees from Neural Networks

G.P. J. Schmitz, C. Aldrich, and F.S. Gouws, "ANN-DT: An Algorithm for Extraction of Decision Trees from Artificial Neural Networks". Transactions on Neural Networks 10 (1999) 1392-1401

Train an MLP or RBF model
Generate more data interpolating input points in the neighborhood of the training data (equivalent to adding noise).
Use NN as an oracle to predict class.
Create DT using CART criteria or alternative criteria (correlation between variation of the network and variation of the attribute) to analyze attribute significance.
Prune the network using CART approach.

A few results so far, first good NN should be created.

OC - Oblique Classifier

Many variants of the oblique tree classifiers: CART-LC, CART-AP, OC-1, OC!LP, OC-1AP ...

For some data results are significantly better, trees are smaller, but rules are less comprehensible - combinations of inputs are used.
There is no comparison between neural methods of rule extraction (with aggregation) and oblique trees so far.

Inductive methods

R. Michalski, "A theory and methodology of inductive learning". Artificial Intelligence 20 (1983) 111-161.

StatLog project book:
D. Michie, D.J. Spiegelhalter and C.C. Taylor, "Machine learning, neural and statistical classification". Elis Horwood, London 1994

Many inductive methods have been proposed in machine learning.

PVM

S. Weiss, 1988
Maximize predictive accuracy of a single condition rule, make exhaustive or heuristic search.
Try combinations of 2 conditions.
Expensive but for small datasets finds very simple rules.

RISE - Rule Induction from a Set of Exemplars (Domingos 1996)

Exemplars are maximally specific rules.

• Loop over rules;
• find the nearest example from the same class not yet covered;
• try to generalize existing rule covering the new case - compute change in accuracy and accept it unless classification decreases;
• if no rule is generalized stop.

Use hybrid similarity function, good for nominal and numerical attributes.

Włodzisław Duch