Understanding the data

Interactive database exploration using multidimensional scaling

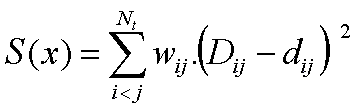
Exploratory data analysis: visualization of data.

• XGOBI "Grand Tour" - projections from different perspective, changing in time.
• Kohonen Maps - perhaps best known, but neither classification nor visualization is correctly done; many variants. Cube 3D; Cube 4D; Cube 5D.
• GTM (Generative Topographic Mapping, Bishop) - mathematically better justified but does not seem to provide such good maps.
• PCA visualization - projection on the most informative linear combination of dimensions.
• Non-linear mappings using MLP with 2-3 hidden neurons.
• Neuroscale (Loewe) - interesting algorithm for topographically correct mapping, based on RBF, minimizing MDS.

Data topography preserving mapping method: MDS (MultiDimensional Scaling)

Idea: try to place images of data vectors in such a way that preserves the distances.

• Minimization of a Stress function as:

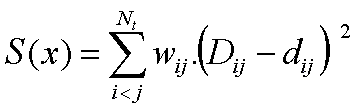
where w_ij are weights allowing to control which distances are to be better preserved.

using a gradient descent method (steepest descent, conjugate gradient, quasi-Newton, ...)

Our choice: steepest descent with 2^nd order optimization of the step-size along the gradient

• Relative Stress expression to map N_m new data points:

• Locally weighted Stress expression to force preservation of distances close to a chosen point P_c:

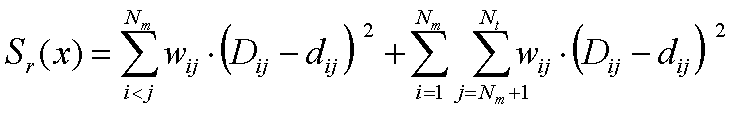
Multiply previous weight w_ij by a Gaussian-like term centered on P_c, decreasing when the mean distance

D_cij = (D_ci + D_cj)/2 between D_ij end points and point P_c is increasing: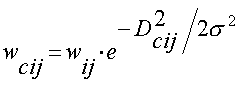

Real life example of a database visualization

Psychometric MMPI test: patients as samples, numerical factors as attributes

Two datasets: Men / Women.

• Women dataset: 1611 samples, 13 attributes, 20 classes
• Men dataset: 1716 samples, 13 attributes, 20 classes

Women dataset

- Purpose: View (Understand) why this data is classified into class 'organika'.

- Classified using IncNet neural network, for which features 2, 4 and 7 are sufficient to classify correctly class 'organika'.

- To avoid interference from noisy dimensions, only those dimensions (2,4,7) were used for the MDS mapping,

• Progressive zooming by mapping successively the 200, 100, 50 and 20 nearest data points (interactively selected) from point 'p554' (marked by a black circled dot).

1 - Generation of 100 new points from a Gaussian distribution centered at p554,

2 - Classification of the new points using IncNet classifier,

3 - Addition of the new points to the 100 nearest neighbors map using relative mapping (each point is mapped separately).

Initialization of the configuration:

• Initialization using the first 2 principal components (SVD of the coordinates matrix),
• Random initialization repeated a number of times,

Our strategy: Initialize using PCA and 20 random trials and then keep the best run.

• When using local minimization method, initial configuration is of crucial importance,
• Small differences in final Stress value may correspond to noticeably different displayed configuration,
• Interactive User Interface implies fast mapping algorithm,
• Reliable mapping implies performant minimization, which implies lengthy procedures,
• A compromise must be found between mapping speed and mapping quality.

• On-line mapping: seeing how the configuration evolves during mapping,
• Possibility to add new points to an existing map using relative mapping,
• Interactive selection of a subset of points: in a rectangle, on a disc of given radius, a N-dimensional sphere,
• Dataset display transformation: translation, rotation, horizontal or vertical flipping and zooming,
• Generation of new points in Gaussians for their classification allows to see classifiers decision borders,
• 'Batch' mapping option: Map in 1 run (all data points together) / Map in x runs (batches of N_t /x points).