,WYK£AD 9
2.2 Oddzia³ywanie świat³a z materią
Odkrycie praw elektrodynamiki i, w konsekwencji, sformu³owanie elektromagnetycznej teorii świat³a przez Maxwella to z pewnością najwa¿niejsze wydarzenie w fizyce XIX wieku. Umo¿liwi³o ono po raz pierwszy, poprzez wykorzystanie pewnych klasycznych modeli materii, wyt³umaczenie wielu zjawisk wywywo³anych przez oddzia³ywanie ró¿nych ośrodków materialnych ze świat³em. Zjawiska te, a tak¿e wyjaśnienie ich w ramach klasycznej elektrodynamiki i klasycznego (niekwantowego) modelowego opisu materii, bêdą celem kilku najbli¼szych wyk³adów.
Pola elektryczne i magnetyczne w pró¿ni i ośrodkach materialnych - równania Maxwella
Klasyczna teoria elektromagnetyzmu opiera siê na równaniach Maxwella, które opisują przestrzenne i czasowe zale¿ności wią¿ące ze sobą pola elektryczne i magnetyczne. Pola te są w zupe³ności opisane przez dwa pola wektorowe, E (natê¿enie pola elektrycznego) i B (indukcjê magnetyczną). Określają one si³ê (tzw si³ê Lorentza), dzia³ającą na dowolny ³adunek q znajdujący siê w pewnym punkcie przestrzeni r i poruszający siê z prêdkością v:
,
co z kolei pozwala na napisanie równañ ruchu i, w konsekwencji, wyznaczenie ruchu pojedynczej na³adowanej cząstki, a zatem tak¿e wiêkszego uk³adu (czy rozk³adu, dla przypadku ciąg³ego) ³adunków.
Poni¿ej przedstawiamy równania Maxwella w postaci ró¿niczkowej (uk³ad SI):
gdzie e 0 to sta³a dielektryczna pró¿ni (przenikalnośæ elektryczna pró¿ni) a sta³a c to prêdkośæ świat³a w pró¿ni. Pierwsze trzy z tych równañ podają prawa, które by³y znane ju¿ przed Maxwellem z badañ nad elektrycznością i magnetyzmem; g³ówna zas³uga Maxwella to, jak chodzi o szczegó³y, dopisanie dodatkowego wyrazu do prawa Ampérea (czwarte równanie), podanie wszystkich równañ razem i, co najwa¿niejsze, wskazanie konsekwencji wynikających ³ącznie ze wszystkich czterech równañ (chodzi oczywiście o istnienie fal elektromagnetycznych). W dwóch pierwszych podrozdzia³ach rozdzia³u 18, tom II, czêśæ 1, Feynman uzasadnia koniecznośæ wprowadzenia dodatkowego wyrazu w czwartym równaniu, w nastêpnych pokazuje jak z pe³nych równañ Maxwella wynika powstawanie i rozchodzenie siê zaburzeñ pól elektycznych i magnetycznych. Chocia¿ w nastêpnych wyk³adach poka¿emy jak mo¿na formalnie otrzymaæ z równañ Maxwella równania falowe dla pól E i B, jednak dyskusja przedstawiona przez Feynmana pozwala na g³êbsze fizyczne zrozumienie co siê w³aściwie dzieje. Wielkości r i j, wystêpujące w równaniach Maxwella to tzw ¼ród³a pól, a konkretnie r oznacza ca³kowitą gêstośæ ³adunku elektrycznego, a j ca³kowitą gêstośæ prądu elektrycznego. W pró¿ni wielkości r i j są dobrze określone i oznaczają po prostu gêstości ³adunków swobodnych i wygenerowanych przez nie prądów (j = r v), natomiast sytuacja komplikuje siê gdy mamy do czynienia z materią. Przyczyna le¿y w tym, ¿e prócz swobodnych ³adunków i pochodzących od nich prądów mamy tak¿e do czynienia z ukrytymi, w pewnym sensie, ³adunkami związanymi, zawartymi w samej materii, a tak¿e z pochodzącymi od nich prądami. Dok³adniejszą dyskusjê i g³êbsze uzasadnienie podaje Feynman (tom II, czêśæ 1, rozdzia³ 10, Dielektryki, tom II, czêśæ 2, rozdzia³ 36, Ferromagnetyzm); tutaj podamy w skrócie najwa¿niejsze kroki prowadzące do zmodyfikowanych równañ Maxwella, w których uwzglêdnienie ³adunków i prądów związanych powoduje wystąpienie dodatkowych pól; pola wektora indukcji elektrycznej zwanego czasem wektorem przesuniêcia D i pola wektora natê¿enia pola magnetycznego H.
W materii umieszczonej w polu elektrycznym E pojawi siê wyindukowany moment dipolowy na jednostkê objêtości P, który bêdzie równy
.
N jest ilością atomów (lub cząsteczek) danej substancji w jednostce objêtości, q jest ³adunkiem dodatnim jednego atomu lub cząsteczki (który, oczywiście, jest zrównowa¿ony przez równy co do wartości ³adunek ujemny), a wektor d przedstawia średnią odleg³ośæ na jaką, pod wp³ywem pola E, rozsuną siê ³adunki dodatnie (+q) i ujemne (-q) w jednym atomie (cząsteczce). Jest oczywiste, ¿e jeśli P = const, przesuniête ³adunki związane kompensują siê dok³adnie w ca³ej objêtości (z wyjątkiem warstwy przypowierzchniowej o grubości rzêdu d ), nie dając wobec tego ¿adnego wk³adu do ca³kowitej przestrzennej gêstości ³adunku r wystêpującej w równaniach Maxwella.
W przypadku niejednorodnej polaryzacji P, sytuacja jest jednak odmienna, niejednorodnośæ ta prowadzi bowiem do pojawienia siê w materiale pewnej wyindukowanej gêstości ³adunku, r pol, takiej, ¿e:
,
która stanowiæ bêdzie czêśæ ca³kowitego ³adunku r w pierwszym równaniu Maxwella:
.
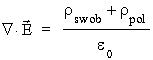Podstawiając za r pol dywergencjê P i grupując odpowiednio wyrazy otrzymamy:
.
Jeśli wprowadzimy nowy wektor D = e 0E + P, to równanie to mo¿emy zapisaæ w prostszej (i nadal zupe³nie ścis³ej) postaci:
,
gdzie jednak uproszczenie jest do pewnego stopnia pozorne; problem ³adunków związanych nie zosta³ bowiem rozwiązany, tylko ukryty w wektorze indukcji D. Warto zwróciæ uwagê, ¿e tak¿e ³adunki swobodne, np elektrony, mogą pochodziæ z atomów czy cząsteczek materia³u (jak w przewodnikach czy pó³przewodnikach prądu), choæ ich obecnośæ musi byæ, w takim przypadku, skompensowana obecnością pewnego dodatniego ³adunku przestrzennego. Praktycznie rozwiązanie tego równania nie jest wcale ³atwe, jest bowiem oczywiste, ¿e polaryzacja P mo¿e w skomplikowany sposób zale¿eæ od pola E. W najprostszym przypadku bêdziemy mieli:
,
gdzie c e jest sta³ą materia³ową zwaną podatnością elektryczną danego materia³u. Mamy wówczas:
,
gdzie sta³a e = 1 + c e /e 0 nazywa siê sta³ą dielektryczną albo przenikalnością elektryczną danego materia³u. Ostatnie dwa równania mają charakter przybli¿ony; są one bowiem próbą opisu pewnych w³asności materia³ów, które, mo¿na sądziæ, mogą byæ bardzo ró¿ne. W szczególności liniowa zale¿nośæ polaryzacji od pola elektrycznego, a tak¿e skalarny charakter podatności elektrycznej i sta³ej dielektrycznej są pewnymi przybli¿eniami, które w konkretnej sytuacji mogą byæ spe³nione lepiej lub gorzej, czasami mo¿e nawet bardzo niedobrze (do tego stopnia, ¿e nie mo¿na tego d³u¿ej lekcewa¿yæ, bo mo¿emy zgubiæ potencjalne wyt³umaczenie obserwowalnych efektów fizycznych).
Podobnie jak obecnośæ materii powoduje, ¿e czêśæ ³adunku, określającego pole E, jest związana z atomami czy cząsteczkami materia³u, mo¿emy tak¿e oczekiwaæ, ¿e czêśæ prądów, określających poprzez czwarte równanie pole magnetyczne B, bêdzie pochodzenia atomowego (czy cząsteczkowego). W szczególności spodziewamy siê takiego wk³adu do ca³kowitego prądu od ³adunków polaryzacyjnych, r pol. Znajdziemy ten wk³ad korzystając z nastêpującego równania:
.
Równanie to wią¿e wyp³yw prądu z danego punktu ze zmianą gêstości ³adunku polaryzacyjnego w tym punkcie, w związku z tym nazywa siê je równaniem ciąg³ości (albo zasadą zachowania ³adunku). Mo¿na je ³atwo wyprowadziæ, biorąc dywergencjê z obu stron czwartego równania Maxwella i wykorzystując równanie pierwsze, a tak¿e fakt, ¿e div(rotF) º 0 dla dowolnego pola F. Podstawiając r pol = -divP i zamieniając kolejnośæ ró¿niczkowania po wspó³rzêdnych przestrzennych i czasie, otrzymamy:
.
W substancjach magnetycznych, w których zewnêtrzne pole magnetyczne wywo³uje silne namagnesowanie M, zdefiniowane jako moment magnetyczny na jednostkê objêtości spodziewamy siê tak¿e istnienia pewnych wewnêtrznych prądów odpowiedzialnych za istnienie momentów magnetycznych, m , związanych z pojedynczymi atomami czy cząsteczkami materia³u (podobnie jak dla polaryzacji dielektrycznej mamy tak¿e w tym przypadku związek M = Nm ). Mo¿na pokazaæ (Feynman, tom II, czêśæ 2, str. 282-289, podrozdzia³ 36-1), ¿e prądy te, które oznaczymy symbolem jmag, wią¿ą siê z wektorem M w nastêpujący sposób:
.
Podstawiając do czwartego równania Maxwella za ca³kowity prąd j = jpol + jmag + jswob, odpowiednie uzyskane wy¿ej wyra¿enia opisujące poszczególne wk³ady do j, otrzymamy:
.
Grupując odpowiednie wyrazy i wykorzystując podaną wy¼ej definicjê wektora D, otrzymamy dalej:
.
£atwo zgadnąæ nasz nastêny krok; oczywiście wprowadzimy nowe pole, H, które bêdzie równe:
,
co pozwoli nam zapisaæ czwarte równanie w nastêpującej uproszczonej postaci:
.
Pole H nazywamy natê¿eniem pola magnetycznego. Podobnie jak w przypadku równania elektrycznego, powy¿sze równanie magnetyczne jest zupe³nie ścis³e i, na pierwszy rzut oka, dośæ proste; k³opot jednak jest, polega on na tym, ¿e nie znamy namagnesowania M, a dok³adniej związku M z H. Przyjmując, ¿e
,
gdzie c m nazwiemy podatnością magnetyczną danego materia³u, a tak¿e wprowadzając nową sta³ą, m 0, zwaną przenikalnością magnetyczną pró¿ni
,
mo¿emy zapisaæ:
.
Przenikalnośæ magnetyczna materia³u m , zdefiniowana powy¿szym wzorem, bêdzie równa:
m = 1 + c m.
Skoro ju¿ przy tym jesteśmy, warto zwróciæ uwagê, związek pomiêdzy przenikalnością magnetyczną i elektryczną pró¿ni pozwala wyliczyæ sta³ą c (obie przenikalności mo¿na wyznaczyæ z pewnych pomiarów elektrycznych i magnetycznych). Jak zobaczymy pó¼niej, sta³a c odpowiada prêdkości rozchodzenia siê zaburzeñ pól elektromagnetycznych w pró¿ni, zaburzeñ, których istnienie wynika z analizy równañ Maxwella. Mo¿emy sobie wyobraziæ, jak przejêty musia³ byæ Maxwell i jemu wspó³cześni, gdy okaza³o siê, ¿e wyliczona sta³a c odpowiada z niez³ą dok³adnością wyznaczonej eksperymentalnie prêdkości świat³a! To by³ naprawdê wielki moment w historii fizyki i, chyba mo¿na tak powiedzieæ, jeden z wa¿niejszych w historii naszej cywilizacji.
Podsumowując, pe³ny opis pól elektromagnetycznych w dowolnym materiale wymaga wprowadzenia czterech pól wektorowych, E, D, H i B, a tak¿e znajomości rozk³adu gêstości i prêdkości ³adunków swobodnych. Równania Maxwella bêdą mia³y postaæ nastêpującą:
Do rozwiązania tych równañ potrzebne są tak¿e związki materia³owe:
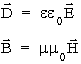
w których wystêpują sta³e materia³owe e i m (przenikalnośæ elektryczna i magnetyczna danego materia³u) a tak¿e e 0 i m 0 (przenikalnośæ elektryczna i magnetyczna pró¿ni). W ogólności sta³e e i m nie muszą byæ skalarami (tzn mogą byæ tensorami, co oznacza, ¿e kierunek wektorów D i B nie musi pokrywaæ siê z kierunkami wektorów E i H), a równania, wią¿ące ze sobą sk³adowe czterech pól, nie muszą byæ koniecznie i w ka¿dym przypadku liniowe.
Energia i moc w polu elektromagnetycznym
Jeśli na pewną cząstkê poruszającą siê z prêdkością v dzia³a si³a F, to moc chwilowa, przekazana przez pole si³y F cząstce wyniesie:
.
Tak wiêc moc chwilowa, tracona przez pole elektromagnetyczne na rzecz uk³adu dyskretnych ³adunków swobodnych wyniesie:
,
gdzie suma przebiega po wszystkich (swobodnych) ³adunkach uk³adu. W przypadku uk³adu, którego opis wymaga wprowadzenia ciąg³ego rozk³adu ³adunku:
,
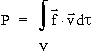gdzie V jest objêtością zajmowaną przez uk³ad, a f gêstością si³y; F = q(E + v´ B) zatem f = r (E + v´ B), gdzie r jest gêstością ³adunku q. Podstawiając za f wyra¿enie na si³ê Lorentza, a tak¿e biorąc pod uwagê, ¿e pole B nie pracuje, v× (v ´ B) = 0, mamy:
.
Skorzystamy teraz z dwóch równañ z rotacją, które pomno¿ymy skalarnie odpowiednio przez wektor E i H:
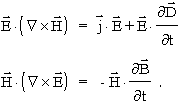
Po odjêciu stronami i wykorzystaniu nastêpujących związków:
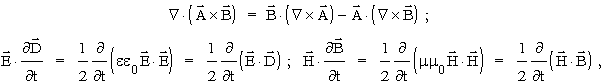
otrzymamy:
.
Po uwzglêdnieniu twierdzenia Gaussa (ca³ka po pewnej objêtości V z dywergencji dowolnego wektora jest równa ca³ce ze sk³adowej normalnej tego wektora po powierzchni S ograniczającej tê objêtośæ; wektor n jest skierowany na zewnątrz):
,
otrzymujemy nastêpujące równanie:
,
w sposób oczywisty przedstawiające bilans energetyczny uk³adu fizycznego (oczywisty, ze wzglêdu na wystêpowanie wyrazu jE, o którym ju¿ powiedzieliśmy, ¿e przedstawia chwilową moc straconą na rzecz uk³adu ³adunków). Z ca³ą pewnością mo¿na by³oby dok³adniej siê przyjrzeæ poszczególnym wyrazom, ale i bez tego mo¿na ju¿ teraz odgadnąæ, ¿e wyraz po lewej stronie przedstawia moc wp³ywającą do uk³adu (ze wzglêdu na znak minus), która, jak wskazuje strona prawa, mo¿e zostaæ zu¿yta na wykonanie pracy nad uk³adem ³adunków swobodnych lub przyczyniæ siê do wzrostu pewnej wielkości, która musi byæ energią pola elektromagnetycznego zawartego w objêtości V.
Tak wiêc wektor S, zwany wektorem Poyntinga i równy:
,
przedstawia gêstośæ mocy (czyli energiê na sekundê i na metr kwadratowy) wp³ywającej do (lub wyp³ywającej z, zale¿nie od znaku ca³ki) uk³adu fizycznego, a wielkośæ u:
przedstawia gêstośæ energii pola elektromagnetycznego. Ca³y bilans zatem przedstawia po prostu zasadê zachowania energii dla uk³adu oddzia³ujących ³adunków i pól elektromagnetycznych.
Dla pró¿ni:
,
a dla pewnego ośrodka materialnego
gdzie za wektory D i B podstawiliśmy wyra¿enia z polaryzacją P i namagnesowaniem M. Widaæ, ¿e po przemno¿eniu wyra¿enie na gêstośæ energii zawieraæ bêdzie szereg ró¿nych wyrazów (a w³aściwie to tylko cztery); sprawd¼my, czy rozumiemy ich sens fizyczny:
.
Znaczenie pierwszych dwóch wyrazów jest oczywiste; przedstawiają one gêstośæ energii pola elektromagnetycznego w pró¿ni. Oczywiście, w naszym przypadku oprócz tych dwóch wyrazów spodziewamy siê tak¿e wk³adu od wyindukowanych w ośrodku, dziêki polom w pró¿ni, E i B0 = m 0H, dipoli elektrycznych i momentów magnetycznych. Poniewa¿ energia potencjalna ka¿dego elementarnego dipola (qd i m , jak je oznaczaliśmy poprzednio) jest równa iloczynowi skalarnemu tego momentu i pola, z którym ten dipol oddzia³uje (jeśli ktoś nie pamiêta tych wzorów, to na pewno znajdzie je w Feynmanie), zatem ca³kowita energia potencjalna ca³ego uk³adu dipoli wyrazi siê poprzez średni moment dipolowy tego uk³adu, a gêstośæ energii potencjalnej wyrazi siê poprzez moment dipolowy na jednostkê objêtości, czyli polaryzacjê lub namagnesowanie. Dok³adnie taką w³aśnie postaæ mają pozosta³e dwa wyrazy w naszym wyra¿eniu na ca³kowitą gêstośæ energii pola elektromagnetycznego w ośrodku materialnym.
Fale elektromagnetyczne w pró¿ni
Zaczniemy od przypadku najprostszego, od pró¿ni. W pró¿ni nie ma ³adunków ani prądów, a wiêc:
Z równañ tych wyeliminujemy najpierw wektory D i H tak, ¿eby otrzymaæ równania na pola E i B; w nastêpnym kroku postaramy siê uzyskaæ dwa niezale¿ne równania, jedno z E, a drugie z B.
Bierzemy rotacjê z obu stron równania drugiego, zmieniamy kolejnośæ ró¿niczkowania i wykorzystujemy równanie czwarte:
.
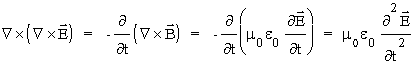Ze wzglêdu na to¿samośæ: rot(rotF) = grad(divF) - Ñ 2F, zachodzącą dla dowolnego pola wektorowego F mamy dalej:
,
(zwróæcie uwagê na ró¿nicê pomiêdzy gradientem z dywergencji pola, a laplasjanem z tego¿ pola). W ostatnim kroku wykorzystamy pierwsze równanie Maxwella (divE = 0) by otrzymaæ równanie:
,
w którym rozpoznajemy równanie falowe, przy czym prêdkośæ fali v bêdzie równa 1/(m 0e 0)1/2 czyli, zgodnie z naszymi wcześniejszymi definicjami, pewnej sta³ej, którą oznaczyliśmy jako c.
Zupe³nie analogicznie, biorąc rotacjê z obu stron równania czwartego, wykorzystując nastêpnie równanie drugie (rotacjê z pola E zastêpujemy pochodną po czasie z pola B) uzyskujemy równanie:
podobnie jak dla pola elektrycznego. W pró¿ni oba pola, B i H, ró¿nią siê tylko sta³ą numeryczną (przenikalnością magnetyczną pró¿ni m 0), zatem powinniśmy tylko pamiêtaæ, ¿e si³a Lorentza wyra¿a siê poprzez pole B, a do opisu fali u¿ywaæ mo¿emy któregolwiek z tych dwóch pól. Podobnie w ośrodkach niemagnetycznych, dla których m = 1 (co oznacza, ¿e c m = 0, zatem namagnesowanie M jest równe zero) ró¿nica miêdzy polami B i H jest ma³o istotna. Sytuacja zmienia siê, gdy namagnesowanie jest znaczące i w istotny sposób wnosi wk³ad zarówno do ca³kowitej gêstości energii pola elektromagnetycznego w danym ośrodku materialnym jak i, byæ mo¿e, transportu ca³kowitej energii uk³adu poprzez ośrodek. Nale¿y jednak pamiêtaæ, ¿e wektor Poyntinga, opisujący strumieñ mocy pola elektromagnetycznego, wyra¿a siê poprzez wektor H a nie B. Rozró¿nienie to, jak ju¿ wspominaliśmy, przestaje byæ wa¿ne dla ośrodków niemagnetycznych (wiêkoszośæ wa¿nych ośrodków rozpatrywanych w optyce to ośrodki niemagnetyczne). Dla wszystkich ośrodków najczêściej (choæ nie wy³ącznie) u¿ywaæ bêdziemy pola B co u³atwia opis oddzia³ywania fali elektromagnetycznej z materią ze wzglêdu, jak ju¿ wspominaliśmy, na postaæ wyra¿enia na si³ê Lorentza.
Monochromatyczne fale p³askie w ośrodkach materialnych
Rozpatrywaæ bêdziemy rozchodzenie siê monochromatycznych (a wiêc harmonicznych, czyli o określonej czêstości) fal elektromagnetycznych w ośrodkach jednorodnych. Ośrodki jednorodne to takie ośrodki, w których wszystkie sta³e materia³owe, e , m , c e i c m, a tak¿e dodatkowa sta³a s , o której wiêcej za chwilê, nie zale¿ą od wspó³rzêdnych przestrzennych. Dla przyk³adu, dziêki za³o¿eniu o jednorodności materia³u mo¿emy np z równania divD = div(e e 0E) = 0 wywnioskowaæ, ¿e divE = 0. Warto zwróciæ uwagê, ¿e za³o¿enie o jednorodności nie jest spe³nione na granicach pomiêdzy ró¿nymi ośrodkami, a wiêc rozpatrując takie zjawiska jak odbicie czy za³amanie świat³a musimy tê niejednorodnośæ wziąæ pod uwagê (co nie jest znowu takie zaskakujące; raczej spodziewamy siê, ¿e skok w³asności fizycznych na granicy pomiêdzy ośrodkami jest istotny dla tych zjawisk).
Do wprowadzonych ju¿ przedtem równañ materia³owych do³ączymy jeszcze jedno równanie o charakterze empirycznym, znane powszechnie jako prawo Ohma:
,
wią¿ące gêstośæ prądu j z natê¿eniem pola elektrycznego E. Sta³a s nosi nazwê przewodnictwa w³aściwego.
Nasze rozwa¿ania rozpoczniemy od ośrodka jednorodnego i izotropowego z prądami i ³adunkami. Równania Maxwella dla takiego ośrodka przyjmą nastêpującą postaæ:
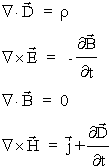
gdzie r i j oznaczają odpowiednio gêstośæ ³adunku i prądy pochodzące od ³adunków swobodnych (upraszczamy oznaczenia; po to w koñcu wprowadzono wektory D i H, ¿eby nie trzeba by³o pamiêtaæ o ró¿nych mo¿liwych rodzajach ³adunków i prądów).
Poniewa¿ rozpatrujemy fale monochromatyczne, szukamy rozwiązañ w postaci:
gdzie indeks dolny s oznacza czêśæ przestrzenną fali. Oscylacyjny charakter prądu wynika z za³o¿enia o oscylacyjnym charakterze pola elektrycznego i z prawa Ohma. Równanie ciąg³ości natomiast mo¿emy wykorzystaæ, ¿eby znale¼æ zale¿nośæ czasową ³adunku. Mamy bowiem:
,
a po sca³kowaniu otrzymujemy:
, a wiêc 
,
gdzie:
.
Mamy tak¿e nastêpujące zale¿ności:
,
a wiêc razem ju¿ wszystko co potrzeba aby, po wykonaniu ró¿niczkowania po czasie i podzieleniu przez czynnik e-iw t, z równañ Maxwella otrzymaæ równania na Es i Hs:
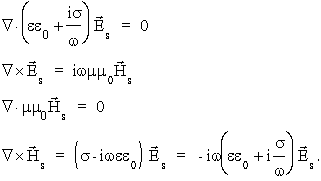
W ośrodku jednorodnym m , e i s nie zale¿ą od wspó³rzêdnych przestrzennych a wiêc dwa równania z dywergencją przyjmą prostszą postaæ:
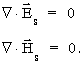
Poniewa¿ szukamy rozwiązañ w postaci fali p³askich przyjmujemy:
,
gdzie kz oznacza zespolony wektor falowy. Czêśæ rzeczywista tego wektora odpowiada wektorowi falowemu k, a nad znaczeniem czêści zespolonej (o ile siê takowa pojawi), zastanowimy siê pó¼niej. Sta³e wektory E0 i H0 przedstawiają zespolone amplitudy oscylacji wektorów pola E i H (wystêpowanie czêści urojonej w amplitudzie oscylacji, jak pamiêtamy, oznacza polaryzacjê eliptyczną).
Poniewa¿ kz× r = kzxx + kzyy + kzzz, dzia³anie operatora Ñ na przestrzenną czêśæ fali p³askiej bêdzie równowa¿ne mno¿eniu przez odpowiednie sk³adowe wektora kz:
Mo¿na zatem ³atwo wykazaæ, ¿e równania z dywergencją przyjmą postaæ z iloczynami skalarnymi, jak ni¿ej:
podczas gdy równania, w których wystêpuje rotacja, bêdą zawiera³y cz³ony z iloczynami wektorowymi wektorów kz i E0 bąd¼ H0:
.
£atwo zauwa¿yæ, ¿e równania te to nie są ju¿ równania ró¿niczkowe, tylko algebraiczne, a wiêc znacznie ³atwiejsze do rozwiązania. Spróbujemy najpierw otrzymaæ równanie na E. Do drugiego równania z iloczynem wektorowym podstawiamy H0 wyliczone z poprzedniego i otrzymujemy w ten sposób równanie na E0:
.
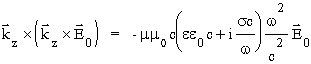Po uporządkowaniu prawej strony i skorzystaniu z to¿samości A´ (B´ C) º (AC)B -(AB)C mamy:
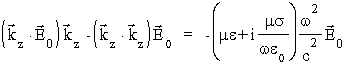
i dalej, poniewa¿ kzE0 = 0,
gdzie za (w
/c)2 podstawiliśmy 
, wprowadzając w ten sposób oznaczenie k0 na wektor falowy w pró¿ni. Równanie to bêdzie spe³nione gdy:
,
gdzie
,
a nz nazwiemy zespolonym wspó³czynnikiem za³amania.
Niech 
i 
, gdzie, jak siê przekonamy za chwilê, n to dobrze nam ju¿ znany (zwyk³y) wspó³czynnik za³amania, sta³ą k
(kappa) nazwiemy wspó³czynnikiem ekstynkcji (wygaszania), k bêdzie wektorem falowym, a a wektorem ekstynkcji albo wygaszania. Mamy wówczas:
skąd wynikają nastêpujące równania, które muszą byæ spe³nione przez cztery sta³e n, k , k i a:
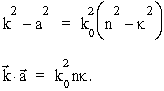
Poniewa¿ liczba zespolona 
ma zawsze dodatnią czêśæ urojoną (wynoszącą m
s
/w
e
0, ewentualny wk³ad do czêści urojonej od e
, choæ mo¼e byæ ujemny jednak jest znacznie mniejszy), charakteryzujący ją na p³aszczy¼nie liczb zespolonych kąt a
musi byæ zawarty pomiêdzy zerem i p
. Zatem kąt liczby zespolonej nz, który bêdzie równy a
/2, musi byæ zawarty pomiêdzy zerem i p
/2, co oznacza, ¿e zarówno czêśæ rzeczywista jak i urojona nz musi byæ nieujemna, czyli wspó³czynniki za³amania n i ekstynkcji k
są zawsze dodatnie lub równe zeru. Stąd wnioskujemy, ¿e tak¿e iloczyn skalarny k×
a musi byæ nieujemny, czyli kąt pomiêdzy wektorami k i a nie mo¿e byæ wiêkszy od p
/2.
Rozumowanie to dopuszcza dwa rozwiązania, jedno bardzo specjalne (k = 0), a drugie (n, k > 0), o charakterze ogólnym.
W pierwszym przypadku mamy:
co oznacza, ¿e albo wektor ekstynkcji a jest prostopad³y do k (przypadek, który pomijamy, nie widzimy w tej chwili dla niego zastosowania fizycznego), albo a = 0. W drugim przypadku (nosi on nazwê rozwiązania jednorodnego) mamy:
i rozwiązanie dla pola elektrycznego w postaci fali p³askiej bêdzie mia³o nastêpującą postaæ:
.
Poniewa¿ k× E0 = k× B0 = 0, wnioskujemy, ¿e oba wektory E i B są prostopad³e do wektora falowego k. Z drugiej strony, poniewa¿:
zatem B musi byæ tak¿e prostopad³e do E. Stąd wniosek, ¿e trzy wektory E, B i k są do siebie wzajemnie prostopad³e. Poniewa¿ k = k0n, a k0 = w /c mamy k = w n/c, a tak¿e:
,
gdzie v jest prêdkością rozchodzenia siê fali elektromagnetycznej w danym ośrodku materialnym.
W drugim przypadku, gdy n, k > 0, mo¿liwe rozwiązanie równañ z k, a, n i k bêdzie mia³o postaæ:
,
co z kolei narzuca nastêpujące rozwiązanie na szukane pole elektryczne fali p³askiej:
.
Jest to rozwiązanie podobne do poprzedniego (tak¿e zwane jednorodnym); przedstawia ono falê p³aską i harmoniczną, ale o t³umionej amplitudzie, E0exp(-a× r). £atwo mo¿na udowodniæ, ¿e tak¿e w tym przypadku B = E/v.
Pokazaliśmy, ¿e w³asności ośrodka materialnego wa¿ne dla zjawiska rozchodzenia siê w tym ośrodku fal elektromagnetycznych zale¿ą od zespolonego wspó³czynnika za³amania nz, który z kolei określony jest przez trzy sta³e materia³owe; e (przenikalnośæ elektryczna), m (przenikalnośæ magnetyczna) i s (przewodnictwo w³aściwe). W takim razie bli¿sze zrozumienie tego zjawiska wymaga modelu ośrodka materialnego, który pozwoli³by powiązaæ parametry materia³owe z jakimiś bardziej elementarnymi sta³ymi czy parametrami, charakteryzującymi dany materia³ lub raczej tworzące go atomy czy cząsteczki.