WYK£AD 8
2. OPTYKA FALOWA
ODDZIAŁYWANIE WIATŁA Z MATERIĽ
2.1 Fale
Opis matematyczny drgañ (oscylacji) - zapis zespolony
Drgania lub inaczej oscylacje to zjawiska zachodzące w dynamicznym uk³adzie fizycznym, w trakcie których obserwujemy zmiany w czasie pewnych wielkości fizycznych charakteryzujących ten uk³ad, jak np wychylenia z po³o¿enia równowagi pewnych elementów uk³adu mechanicznego, natê¿enia prądu lub napiêcia w uk³adzie elektrycznym, ciśnienia w zbiorniku gazu itd. Zmiany te mogą zachodziæ w sposób powtarzalny (mówimy wtedy o drganiach okresowych lub periodycznych) lub niepowtarzalny (drgania nieokresowe). Szczególnym i bardzo wa¿nym przypadkiem drgañ okresowych są tzw drgania harmoniczne opisane funkcją cosinus (lub sinus):
![]() drganie liniowe punktu materialnego
drganie liniowe punktu materialnego
![]() oscylacja wielkości skalarnej p
oscylacja wielkości skalarnej p
![]() trójwymiarowa oscylacja punktu materialnego
trójwymiarowa oscylacja punktu materialnego
![]() oscylacja harmoniczna wielkości wektorowej.
oscylacja harmoniczna wielkości wektorowej.
W podanych wy¿ej przyk³adach drgañ harmonicznych wystêpują pewne wielkości wspólne jak np amplituda (![]()
![]() ,
, ![]()
![]() ), prêdkośæ kątowa w
i czas t (ich iloczyn nazywamy fazą); w ogólności mo¿e wystąpiæ dodatkowo tzw faza początkowa
), prêdkośæ kątowa w
i czas t (ich iloczyn nazywamy fazą); w ogólności mo¿e wystąpiæ dodatkowo tzw faza początkowa ![]() (jak w ostatnim przyk³adzie), a funkcja opisująca zmiany wielkości fizycznej mo¿e byæ tak¿e przedstawiona jako funkcja sinus.
(jak w ostatnim przyk³adzie), a funkcja opisująca zmiany wielkości fizycznej mo¿e byæ tak¿e przedstawiona jako funkcja sinus.
Stosowanie zapisu zespolonego opiera siê na tzw równośæ Eulera 1):
![]() ,
,
gdzie ![]() , dziêki której, dla przyk³adu, pewna funkcja z, o wartościach danych liczbami zespolonymi o module x0 i fazie w
t mo¿e byæ przedstawiona w postaci:
, dziêki której, dla przyk³adu, pewna funkcja z, o wartościach danych liczbami zespolonymi o module x0 i fazie w
t mo¿e byæ przedstawiona w postaci:
![]() .
.
_____________________________________________________________________
1)
Hecht podaje nastêpujące wyprowadzenie tej równości: ró¿niczkujemy wyra¿enie z = cosq + isinq i otrzymujemy dz = (-sinq +icoswq)dq = izdq. Stąd dz/z = idq, zatem ln z = iq i dalej z = ei q. To podejście jest byæ mo¿e bardzo dobre dla tych, co nie chcą traciæ du¿o czasu a muszą mieæ wszystko wyprowadzone. Feynman poświêca równości Eulera ca³y rozdzia³ 22 w tomie I, gdzie wprowadza ją w bardzo interesującym i szerokim kontekście; przeczytajcie, jak chcecie zobaczyæ jak wielki fizyk podchodzi do matematyki. Kolejny rozdzia³ Feynmana, 23, to bardzo dobre wprowadzenie do zapisu zespolonego ._____________________________________________________________________
Stąd wynika, ¿e czêśæ rzeczywista tej funkcji, Re(z), przedstawia drganie liniowe i harmoniczne punktu materialnego w normalnym zapisie:![]()
gdzie x0 gra rolê amplitudy drgañ punktu materialnego. Odwracając ca³ą sprawê mo¿emy zatem powiedzieæ, ¿e drganiu x0 cos(w t + f 0) odpowiadaæ bêdzie pewna funkcja zespolona
![]()
gdzie nowa zespolona amplituda zawiera w sobie informacjê o fazie początkowej f 0 i której czêśæ rzeczywista opisuje realne fizyczne drganie punktu materialnego.
Aby porównaæ u¿ytecznośæ obu zapisów w konkretnych rachunkach obliczymy rezultat z³o¿enia dwóch liniowych i harmonicznych drgañ o tej samej czêstości ko³owej ale ró¿nej fazie początkowej:
![]() ,
,
gdzie ![]() a
a ![]()

Wykorzystaliśmy tutaj fakt, ¿e czêśæ rzeczywista sumy dwóch liczb zespolonych to jest sumą czêści rzeczywistych tych liczb, a tak¿e nastêpujące wyra¿enia:
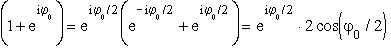 ,
,
otrzymane w wyniku prostych przekszta³ceñ i zastosowania wzoru Eulera.
Zatem, poniewa¿ fizyczne drganie jest reprezentowane przez czêśæ rzeczywistą drgania wypadkowego w opisie zespolonym mamy ostatecznie:
![]() ,
,
wynik, który by³by z pewnością du¿o trudniejszy do uzyskania przy u¿yciu reprezentacji cosinusowej i konwencjonalnych wzorów trygonometrycznych (bez poradnika z matematyki byæ mo¿e mielibyśmy trudności z przypomnieniem sobie wzorów na cosinusy i sinusy sumy kątów, wzorów na kąty po³ówkowe itd). Tak nawiasem mówiąc, skoro ju¿ dostaliśmy jakiś wynik, to chyba warto choæ trochê na niego popatrzeæ: mamy tutaj wypadkową oscylacjê (czêsto mówimy, ¿e jest to superpozycja oscylacji sk³adowych) o tej samej czêstości co drgania sk³adowe, o fazie początkowej równej średniej faz początkowych i o amplitudzie, której wielkośæ zale¿y od ró¿nicy faz drgañ sk³adowych. Dla zerowej ró¿nicy faz drganie wypadkowe ma maksymalną amplitudê 2x0, a dla ró¿nicy faz równej p amplituda wypadkowa jest równa zero (drgania sk³adowe znoszą siê dok³adnie, co ³atwo sobie wyobraziæ).
Bardzo wa¿nym warunkiem stosowania zapisu zespolonego jest niezale¿nośæ czêści rzeczywistych (którym przypisujemy sens fizyczny) od czêści urojonych (które interpretacji fizycznej nie maja). Warunek ten jest spe³niony dla dodawania (oczywiście tak¿e odejmowania) liczb zespolonych skąd wynika mo¿liwośæ stosowania zapisu zespolonego do sk³adania drgañ. Warunek niezale¿ności jest spe³niony tak¿e w wielu innych przypadkach; bêdziemy o tym mówili w ka¿dym przypadku, na który natrafimy.
Rozpatrzymy teraz dok³adniej przypadek trójwymiarowych harmonicznych drgañ punktu materialnego, którego po³o¿enie opisane jest wspó³rzêdnymi kartezjañskimi x, y i z:
![]()
![]() ,
, ![]()
gdzie trzy amplitudy a1, a2 i a3, a tak¿e trzy fazy początkowe q 1, q 2 i q 3 mogą mieæ dowolne wartości (oczywiście rzeczywiste). Jeśli wprowadzimy trzy wektory jednostkowe skierowane wzd³u¿ osi uk³adu to po³o¿enie punktu materialnego mo¿emy opisaæ wektorem:
![]() ,
,
który stanowi czêśæ rzeczywistą nastêpującego wektora zespolonego:
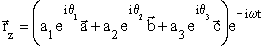 ,
,
bêdącego reprezentacją zespoloną trójwymiarowej oscylacji punktu materialnego. Zespolony wektor ![]() mo¿emy przedstawiæ w innej postaci:
mo¿emy przedstawiæ w innej postaci:
![]() ,
,
gdzie:
 .
.
Wektor A + iB nazywamy zespoloną amplitudą drgania. Jak widaæ ka¼demu zbiorowi amplitud i faz początkowych opisujących oscylacjê ka¿dej sk³adowej kartezjañskiej odpowiada para rzeczywistych wektorów A i B. Rzeczywista czêśæ wektora rz mo¿e byæ w takim razie zapisana w innej postaci:
![]() ,
,
z której wynika jednoznacznie, ¿e koniec wektora r opisujący po³o¿enie punktu materialnego porusza siê po torze le¿ącym w p³aszczy¼nie wyznaczonej przez wektory A i B (rys. 29). Mo¿na udowodniæ, ¿e tor ten opisany jest elipsą wpisaną w równoleg³obok o bokach równoleg³ych do wektorów A i B.
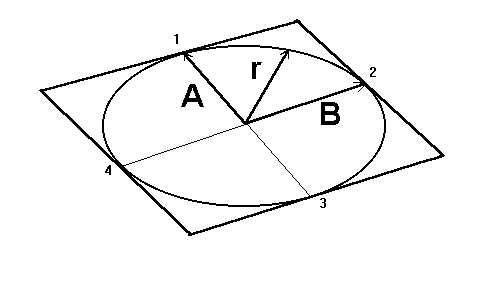
Rys. 29. Związek pomiêdzy torem punktu materialnego wykonującego oscylacjê trójwymiarową o czêstości ko³owej w a rzeczywistą A i urojoną B czêścią zespolonego wektora amplitudy drgañ (A + i B) w zapisie zespolonym. Wektory A i B wyznaczają osie sprzê¿one elipsy-toru, po którym porusza siê punkt materialny. Elipsa ta jest wpisana w równoleg³obok wyznaczony przez wektory A i B.
Wybierzmy uk³ad wspó³rzêdnych w p³aszczy¼nie wyznaczonej przez wektory A i B i oznaczmy wspó³rzêdne kartezjañskie punktu materialnego w tym uk³adzie literami x i h . Mamy wówczas:
 .
.
Wyznaczając z pierwszego równania cos(w t) i wstawiając do drugiego równania, nastêpnie wyliczając sin(w t) otrzymamy:
 .
.
Ze wzglêdu na symetriê równañ na x i h mo¿na ³atwo odgadnąæ, ¿e:
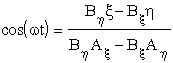
i poniewa¿ cos2(w t) + sin2(w t) = 1 otrzymamy:
 .
.
Choæ na pierwszy rzut oka wyra¿enie to wygląda prawie na kanoniczną postaæ elipsy, w rzeczywistości sporo do tej postaci niestety brakuje. Mimo tego ³atwo mo¿na zauwa¿yæ, ¿e sprowadza siê ono do postaci: ax2 + by2 +cxy = d, gdzie a, b, c i d to pewne sta³e, tak wiêc krzywa opisana tym wyra¿eniem jest drugiego stopnia i musi byæ, wobec tego, krzywą sto¿kową. Z drugiej strony z postaci r = Acos(w t) + Bsin(w t) wynika, ¿e d³ugośæ wektora r nie mo¿e przekroczyæ pewnej wartości maksymalnej poniewa¿ sk³adowe wektorów A i B mają oczywiście sta³e określone wartości, a funkcje sinus i cosinus są ograniczone. Jedyną ograniczoną na p³aszczy¼nie krzywą sto¿kową jest tymczasem elipsa, tak wiêc wnioskujemy, ¿e rozwa¿ana przez nas krzywa musi byæ elipsą.
£atwo zauwa¿yæ, ¿e w chwili t = 0 po³o¿enie wektora r bêdzie r = A a w chwili t = p /2t, r = B. Z drugiej strony styczna do toru prêdkośæ punktu materialnego wyrazi siê wzorem:
![]() ,
,
a wiêc dla t = 0 mamy v = w B, a dla t = p /2t v = -w A. Oznacza to, ¿e w punktach oznaczonych kolejno 1, 2, 3 i 4 na rys. 26 tor punktu materialnego jest styczny do boków równoleg³oboku wyznaczonych przez wektory A i B. W ten sposób odkryliśmy wa¿ną i bardzo wygodną interpretacjê zespolonej wektorowej amplitudy trójwymiarowej oscylacji punktu materialnego; jej czêśæ rzeczywista i zespolona to dwa wektory (A i B) jednoznacznie wyznaczające równoleg³obok, w który wpisany jest tor punktu materialnego opisany elipsą. Wektory A i B wyznaczają osie sprzê¿one tej elipsy.
Fale
Drgania czy oscylacje, o których mówiliśmy do tej pory mia³y charakter lokalny, tzn dotyczy³y pojedynczego punktu materialnego czy zmian pewnej wielkości fizycznej w jednym punkcie przestrzeni. Ale oczywiście istnieją drgania zachodzące w wiêkszym obszarze w pewien skorelowany sposób; takie drgania nazywaæ bêdziemy falami. Tak wiêc nie nazwiemy falą drgañ wykonywanych przez nawet bardzo du¿y zbiór i bardzo ³adnie rozmieszczonych w przestrzeni, ale niepowiązanych ze sobą (mówimy nieoddzia³ujących albo niesprzê¿onych), wahade³ czy ciê¿arków na sprê¿ynkach. Jeśli jednak wymienione wy¿ej ciê¿arki po³ączymy ze sobą nawzajem dodatkowymi sprê¿ynkami to ³atwo sobie wyobraziæ (albo sprawdziæ eksperymentalnie), ¿e wzbudzenie drgañ jednego ciê¿arka spowoduje po pewnym czasie drgania innych; krótko mówiąc powstanie pewne, rozchodzące siê w uk³adzie oddzia³ujących (albo sprzê¿onych) oscylatorów, zaburzenie, które nazwiemy falą. Przy okazji, model sprzê¿onych ze sobą mechanicznych oscylatorów to model, który stosujemy do opisu drgañ i fal (zwanych fononami) sieci krystalicznej w ciele sta³ym. Fale i drgania to zjawiska fizyczne, które są ze sobą ściśle powiązane; ka¿da fala to po prostu nawzajem od siebie uzale¿nione drgania czy oscylacje w ró¿nych punktach przestrzeni; prawie ka¿dej zaś oscylacji towarzyszy wywo³ywana przez nie fala (tak jest z drgającymi ³adunkami elektrycznymi czy prądami, które wywo³ują fale elektromagnetyczne; podobnie jest tak¿e z falami grawitacyjnymi, które towarzyszą drganiom mechanicznym).
Tak wiêc, o ile oscylacjê pewnej wielkości fizycznej y mo¿na opisaæ przy pomocy funkcji jednej zmiennej, podającej zale¿nośæ tej wielkości od czasu t, to opis fali wymaga funkcji dwóch zmiennych, przestrzennej r i czasowej t. Mamy wiêc:
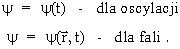
Fale p³askie
Dla jednowymiarowej fali bie¿ącej zmienna przestrzenna, powiedzmy x, i czasowa t, są ze sobą powiązane nastêpującą zale¿nością:
x = x - vt ,
która opisuje transformacjê z nieruchomego uk³adu S do uk³adu S poruszającego siê z prêdkością rozchodzenia siê fali v i w kierunku rozchodzenia siê fali. Mamy wtedy:
![]()
gdzie funkcja f(x) nie zale¿y od czasu i przedstawia profil zaburzenia wielkości fizycznej y rozchodzącego siê w uk³adzie S z prêdkością v, tak jak pokazuje rys. 30. W uk³adzie S zaburzenie jest nieruchome. W uk³adzie S wielkośæ fizyczna y w pewnym wybranym punkcie x przyjmuje wartości określone przez przechodzący przez ten punkt z prêdkością v profil zaburzenia y . Warto zauwa¿yæ, ¼e jeśli wartośæ funkcji f jest określona w ca³ej przestrzeni przez wartośæ wspó³rzêdnej x, a nie zale¿y od pozosta³ych wspó³rzêdnych y i z; to bêdzie ona taka sama na ca³ej p³aszczy¼nie prostopad³ej do osi x. Stąd bierze siê nazwa fala p³aska. Formalizm dla fal jednowymiarowych (czyli rozchodzących siê w uk³adach jednowymiarowych, jak np s³ynny sznurek) i dla p³askich przestrzennych fal skalarnych jest taki sam.

Rys. 30. Zmiany w czasie i przestrzeni wielkości fizycznej y . Pokazano dwa profile tej wielkości, linią przerywaną oznaczono profil w chwili t = 0, a ciąg³ą, w pó¼niejszej chwili t.
Podobnie jak oscylacje, tak¿e fale mogą byæ periodyczne albo, w szczególnym wypadku harmoniczne, wtedy mianowicie gdy:
![]()
gdzie, aby uniezale¿niæ siê od jednostek, w których mierzymy odleg³ośæ wprowadzamy wielkośæ k, zwaną liczbą falową, o wymiarze cm-1, zdefiniowaną jako odwrotnośæ pewnej charakterystycznej d³ugości l , pomno¿onej przez 2p (k = 2p /l ). Argument funkcji cosinus jest wtedy wyra¿ony tak jak nale¿y, w radianach, dodatkowo zaś, ze wzglêdu na sta³ą przy czasie t mamy:
kv = w czyli k = w /v.
Poniewa¿ czêstośæ ko³owa w = 2p /T, gdzie T jest okresem oscylacji mamy k = 2p /Tv no i, ze wzglêdu na definicjê k, k = 2p /l , otrzymujemy l = vT. To ostatnie wyra¿enie nadaje wielkości l znaczenie okresu przestrzennego nazywanego po prostu d³ugością fali. Obserwując falê harmoniczną w pewnym punkcie przestrzeni, x, zauwa¿ymy, ¿e po czasie T wartości wielkości fizycznej y bêdą siê powtarzaæ, f(x,t+T) = f(x,t), co odpowiada przesuniêciu siê przez punkt x pe³nego okresu przestrzennego profilu zaburzenia, równego vT, w tym przypadku funkcji cosinus. Zatem f(x+l ,t) = f(x,t) a okresy przestrzenne T i l , albo inaczej czêstośæ ko³owa w i liczba falowa k są ze sobą ściśle powiązane:
![]() .
.
Tak jak dla oscylacji, mo¿emy i w tym przypadku ³atwo wprowadziæ zapis zespolony dodając do cosinusa reprezentującego fizyczną falê odpowiadającą jej czêśæ urojoną z sinusem:

Dalsze uogólnienie tego zapisu, który przedstawia na razie skalarną bie¿ącą p³aską falê jednowymiarową, to uniezale¿nienie kierunku rozchodzenia siê fali od osi x przez wprowadzenie zmodyfikowanego wyra¿enia na fazê:
![]()
gdzie k jest wektorem falowym, wskazującym kierunek rozchodzenia siê fali (d³ugośæ wektora k wynosi oczywiście k) a r jest wspó³rzêdną przestrzenną. Jasne, ¿e dla k skierowanego wzd³u¿ osi x, mamy kr = kx i wszystko sprowadza siê do rozpatrywanego przez nas przedtem przypadku jednowymiarowego. Narzucając warunek sta³ej fazy otrzymamy równanie wią¿ące ze sobą wektor falowy k i wspó³rzêdną r:
![]() ,
,
skąd, dla określonej chwili t mamy:
![]() .
.
Z geometrii analitycznej pamiêtamy, ¿e równanie Ax +By + Cz + D = 0 przedstawia p³aszczyznê w przestrzeni, wektor N(A,B,C) jest prostopad³y do tej p³aszczyzny a wielkośæ D, podzielona przez d³ugośæ wektora N, czyli (A2 + B2 + C2)1/2, jest równa odleg³ości p³aszczyzny od początku uk³adu wspó³rzêdnych. Oczywiście w miarê up³ywu czasu, który powoduje wzrost wielkości w t, zachowanie sta³ej fazy wymaga kompensującego wzrostu wielkości k× r, czyli odleg³ości (z dok³adnością do d³ugości wektora k) p³aszczyzny od początku uk³adu wspó³rzêdnych. Odpowiada to przesuwaniu siê w przestrzeni ca³ego profilu fali, oczywiście z prêdkościa poruszania siê fali v. Sta³ośæ fazy x gwarantuje dla rozpatrywanej fali sta³ośæ wartości funkcji cosinus, zatem sta³ośæ wielkości fizycznej y . Poniewa¿ powierzchnie sta³ej fazy to p³aszczyzny, zatem te same p³aszczyzny bêdą tak¿e p³aszczyznami sta³ej wartości rozchodzącego siê zaburzenia, tak samo jak dla przypadku jednowymiarowego (dalej mamy do czynienia z falami p³askimi). Warto jeszcze raz przypomnieæ, ¿e w przypadku fali skalarnej, zespolonej amplitudzie y 0 odpowiada pewna początkowa faza j 0 co wynika z faktu, ¿e zespoloną amplitudê mo¿na przedstawiæ w postaci amplitudy rzeczywistej pomno¿onej przez czynnik z j 0:
![]() ,
,
Dla fali wektorowej, zespolona wektorowa amplituda A + iB określa eliptyczny tor, po którym porusza siê koniec pewnego wektora. Z kolei wektor ten opisuje wektorową wielkośæ fizyczną, której zaburzenie rozchodzi siê w uk³adzie w postaci rozpatrywanej przez nas fali.
Dla fal harmonicznych wielkości k i w są dobrze określone i faza mo¿e byæ wyra¿ona nastêpującym wzorem:
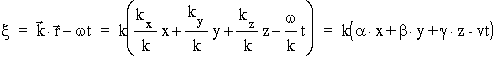 ,
,
gdzie a , b i g to tzw cosinusy kierunkowe (cosinusy kątów pomiêdzy kierunkiem wyznaczonym przez wektor k i osiami uk³adu wspó³rzêdnych x, y i z). Z powy¼szego wzoru widaæ, ¿e argument funkcji kszta³tu dla p³askiej fali nieharmonicznej, dla której wektor falowy k i czêstośæ ko³owa w nie są określone, mo¿e byæ dany nastêpującym wyra¿eniem:
![]()
które, dla trójwymiarowej fali p³askiej rozchodzącej siê w kierunku osi x, wobec a = 1, b = 0 i g = 0, poprawnie sprowadzi siê do x - vt, wyra¼enia, którego u¼ywaliśmy ju¿ przedtem dla fali jednowymiarowej.
Równanie falowe
Wyprowadzenie równania falowego dla ka¿dego przypadku wymaga w³aściwie innego podejścia uwzglêdniającego specyfikê uk³adu fizycznego, chocia¿ czêsto okazuje siê, ¿e postaæ tego równania jest dok³adnie taka sama. Feynman w tomie I, czêśæ 2, rozdzia³ 47 wyprowadza równanie falowe dla fal akustycznych, z równañ Maxwella mo¿na z kolei wyprowadziæ równanie dla fal elektromagnetycznych itd. Je¿eli, tak jak poprzednio, y jest pewną wielkością fizyczną określoną w przestrzeni i czasie, wielkością, której zaburzenie rozchodzi siê w postaci fali p³askiej:
![]() ,
,
to poka¿emy, ¿e dla dowolnego profilu fali f(x) bêdzie spe³nione nastêpujące równanie:
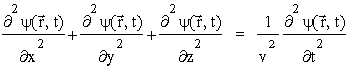 ,
,
w skrócie:
 ,
,
albo, jeszcze inaczej
 .
.
Równanie to (niezale¿nie od postaci) nazywamy równaniem falowym, a operator D º Ñ 2 º ¶ 2/¶ x2 + ¶ 2/¶ y2 + ¶ 2/¶ z2 - laplasjanem.
Aby udowodniæ, ¿e funkcja ![]() spe³nia równanie falowe musimy policzyæ odpowiednie pochodne:
spe³nia równanie falowe musimy policzyæ odpowiednie pochodne:
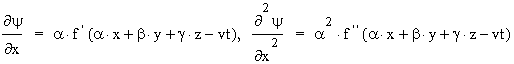 ,
,
gdzie f i f to odpowiednio pierwsza i druga pochodna funkcji f (funkcja f jest w rzeczywistości funkcją jednej zmiennej choæ jest to funkcja z³o¿ona; za tê zmienną jest bowiem podstawione ca³e z³o¿one wyra¿enie z cosinusami kierunkowymi, wspó³rzêdnymi x, y i z, z prêdkością v no i z czasem t). Dla pozosta³ych dwóch zmiennych przestrzennych:
 .
.
Poniewa¿:

otrzymujemy:

z drugiej zaś strony:
 ,
,
a wiêc ostatecznie:
 .
.
Poniewa¿ konkretna postaæ funkcji f (poza warunkiem istnienia pierwszej i drugiej pochodnej) nie by³a dla dowodu wa¿na (sinus te¿ móg³by byæ), mo¿na stąd wyciągnąæ wniosek, ¿e ka¿da funkcja z argumentem w postaci a x + b y + g z -vt (tzn ka¿da fala p³aska) spe³nia równanie falowe. Mo¿na tak¿e pokazaæ, ze jeśli dwie dowolne funkcje, powiedzmy f1(a x+b y+g z-vt) i f2(a x+b y+g z-vt), są rozwiązaniami równania falowego, to jest nim tak¿e funkcja:
F(x,y,z,t) = C1 f1(a x+b y+g z-vt) + C2 f2(a x+b y+g z-vt).
Jest to tzw zasada superpozycji: kombinacja liniowa rozwiązañ równania falowego z dowolnymi wspó³czynnikami sta³ymi jest tak¿e jego rozwiązaniem.
Fale kuliste
Fale p³askie są przybli¿eniem dobrym w sytuacji, gdy ¼ród³o fali znajduje siê bardzo daleko w porównaniu z odleg³ościami wystêpującymi w rozpatrywanym uk³adzie fizycznym (fala wysy³ana przez ¼ród³o bêdzie dok³adnie falą p³aską dla ¼ród³a nieskoñczenie daleko od uk³adu). Czêsto jednak, gdy odleg³ośæ od ¼ród³a nie jest wystarczająco du¼a, stosujemy inne przybli¿enie; tzw przybli¿enie fali kulistej.
Wybieramy uk³ad wspó³rzêdnych sferycznych r, f i q ; spodziewamy siê, ¿e uk³ad ten bêdzie wygodniejszy w sytuacji, gdy ¼ród³o fali znajduje siê w początku uk³adu. Poniewa¿ ¿aden kierunek nie jest, wobec tego, wyró¿niony, oczekujemy, ¿e funkcja y bêdzie zale¿na tylko od wspó³rzêdnej r, a nie od kątów f i q , tzn y (r,t) = y (r,t) (dlatego, choæ wydaje siê to dośæ osobliwe, okazuje siê, ¿e nie potrzebujemy nawet wiedzieæ, jak konkretnie definiuje siê te inne wspó³rzêdne i jaki jest ich związek ze wspó³rzêdnymi kartezjañskimi). Warto zwróciæ uwagê, ¿e bêdzie to z pewnością inny rodzaj fali, ni¿ fala p³aska, którą rozpatrywaliśmy poprzednio; powierzchnie sta³ej fazy bêdą bowiem powierzchniami sferycznymi a nie p³aszczyznami (spodziewamy siê argumentu postaci r-vt, czyli (x2 +y2 +z2)1/2 -vt, a nie x-vt, czy te¿ a x+b y+g z-vt).
Powstaje zatem uzasadnione pytanie, czy po tych wszystkich zmianach funkcja y (r,t) bêdzie nadal spe³niaæ równanie falowe. Przyjmijmy na razie, ¿e tak jest i sprawd¼my konsekwencje naszego za³o¿enia.
Zatem:
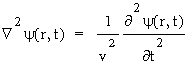 .
.
Poniewa¿ wspó³rzêdne kartezjañskie wystêpują w funkcji y poprzez r, r = (x2 +y2 +z2)1/2, pochodne potrzebne do wyliczenia laplasjanu bêdą mia³y nastêpującą postaæ:
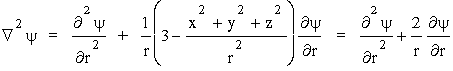 itd.
itd.
Mamy wiêc:
 ,
,
wynik, który jest równowa¿ny nastêpującemu wyra¿eniu:
 ,
,
gdy¿:
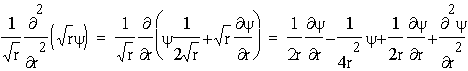 .
.
Po podstawieniu do równania falowego mamy:

i, po pomno¿eniu obu stron przez r:
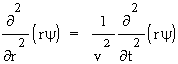 .
.
Otrzymaliśmy w ten sposób równanie, które jest jednowymiarowym równaniem falowym. Oznacza to, ¿e rozwiązaniem tego równania mo¿e byæ dowolna funkcja z w³aściwie dobranym argumentem (chcia³oby siê powiedzieæ, funkcja opisująca falê p³aską), tak jak siê spodziewaliśmy:
![]() .
.
Jednak zale¿nośæ samej funkcji y (r,t) od r i t jest bardziej skomplikowana:
![]() .
.
Jedno z rozwiązañ (ze znakiem minus) przedstawia falê rozbie¿ną (emitowaną przez ¼ród³o punktowe) a drugie (ze znakiem +), falê zbie¿ną do punktu (wiemy z optyki geometrycznej, ¿e ³atwo mo¿na uzyskaæ takie fale świetlne, stosując soczewki skupiające).
W szczególności kulista fala harmoniczna bêdzie opisana w sposób nastêpujący:
![]()
lub, w zapisie zespolonym:
![]() ,
,
gdzie y 0/r przedstawia amplitudê fali, która, inaczej ni¿ dla fali p³askiej, zale¿y od odleg³ości od ¼ród³a r. Podkreślaliśmy ju¿ tak¿e przedtem, ¿e powierzchnie sta³ej fazy, inaczej ni¿ dla fali p³askiej, bêdą mia³y postaæ koncentrycznych powierzchni sferycznych, a nie p³aszczyzn.
Ostatnią klasą rozwiązañ równania falowego, którą omówimy, są fale walcowe (cylindryczne).
Fale walcowe
Fale walcowe są wytwarzane przez ¼ród³a liniowe; mo¿emy oczekiwaæ takich fal po przejściu fali p³askiej przez nieskoñczenie d³ugą i bardzo wąską szczelinê (sytuacjê taką w przypadku świat³a rozwa¿ymy dok³adniej w przysz³ości).
Postêpujemy podobnie jak w przypadku fal kulistych; zak³adamy, ¿e funkcja y (r,t) ma symetriê walcową (tzn y (r,t) = y (r,t), gdzie r = (x2 +y2)1/2, a oś z jest osią symetrii walca, a tak¿e ¼ród³em fali. Obliczamy laplasjan funkcji y (r,t):
 ,
,
podobnie dla sk³adowej y (ale ju¿ nie dla z) i dalej, dodając razem pochodne po x i y:
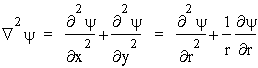 .
.
Wyka¿emy teraz, ¿e dla du¿ych r prawa strona jest równa 
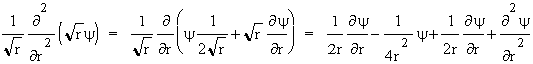
 .
.
Dla du¿ych r, kiedy w porównaniu z poprzednimi mo¿emy pominąæ ostatni wyraz, mamy:
 ,
,
dalej, jeśli równanie falowe ma byæ spe³nione musi zachodziæ:
 ,
,
a wiêc po pomno¿eniu obu stron przez ![]() :
:
 .
.
Otrzymaliśmy znowu jednowymiarowe równanie falowe, zatem:
![]()
i ostatecznie:
![]() .
.
Dla walcowej fali harmonicznej i rozbie¿nej:
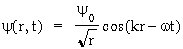 ,
,
a w zapisie zespolonym:
 .
.
Dla fal walcowych amplituda maleje zatem wolniej z odleg³ością ni¿ dla fal kulistych. Nale¿y tak¿e pamiêtaæ, ¿e powy¿sze rozwiązanie jest przybli¿one; otrzymaliśmy je po pominiêciu wyrazu malejącego z kwadratem odleg³ości r, zatem obowiązuje ono tylko dla du¿ych odleg³ości r.