WYK£AD 7
1.7 Zastosowania rachunku macierzowego
Zastosujemy teraz rachunek macierzowy do problemu, który rozwa¿aliśmy ju¿ jakiś czas temu; mianowicie do soczewki grubej. Jak pamiêtamy soczewka gruba sk³ada siê z dwóch powierzchni ³amiących (o mocach optycznych P1 i P2) przedzielonych warstwą ośrodka o wspó³czynniku za³amania n (przyjmiemy, ¿e wspó³czynnik za³amania powietrza wynosi 1), tak jak pokazano na rys. 27.
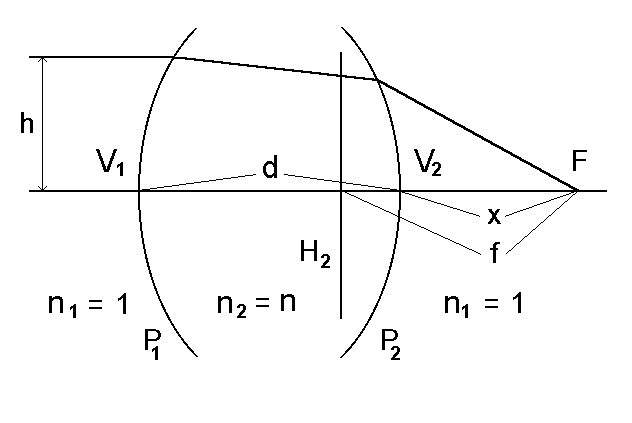
Rys. 27. Soczewka gruba w powietrzu. Dwie powierzchnie ³amiące o mocach optycznych P1 i P2 przedzielone są warstwą ośrodka gêstszego o wspó³czynniku za³amania n i grubości d.
Liczymy macierz soczewki grubej, czyli rozpatrywanego uk³adu optycznego, jako iloczyn macierzy elementów uk³adu:
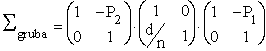
i po przemno¿eniu macierzy sk³adowych otrzymujemy:
 .
.
Niech na soczewkê pada promieñ wejściowy o kącie nachylenia 0 i wysokości h, tak jak pokazano na rys. 27. Mno¿ąc macierz soczewki grubej przez jednokolumnową i dwuwierszową macierz promienia wejściowego otrzymamy (tak¿e jednokolumnową i dwuwierszową) macierz promienia wychodzącego z uk³adu (na drugiej powierzchni ³amiącej):
 ,
,
do której dok³adamy macierz translacji w powietrzu o d³ugośæ x
 ,
,
i znajdujemy w ten sposób macierz promienia wyjściowego, który ma przeciąæ oś optyczną (ognisko) dla odpowiedniej (szukanej i na razie nieznanej) wartości x (liczonej od powierzchni ³amiącej). W punkcie przeciêcia oś - promieñ oczywiście wysokośæ promienia jest równa zeru, zatem
![]() .
.
Warto zauwa¿yæ, ¿e spe³nienie tego warunku jest niezale¿ne od wysokości promienia wejściowego h, zatem wszystkie promienie równoleg³ej wiązki padającej na soczewkê grubą przetną oś optyczną w punkcie F (patrz rys. 27), co oznacza, ¿e punkt F jest obrazowym ogniskiem tej soczewki. £atwo znajdujemy, ¿e po³o¿enie ogniska wzglêdem powierzchni ³amiącej x bêdzie:

Jeśli przyjmiemy, ¿e druga p³aszczyzna g³ówna H2 le¿y w odleg³ości ![]() od drugiej powierzchni ³amiącej o mocy optycznej P2 to
od drugiej powierzchni ³amiącej o mocy optycznej P2 to ![]() , a wielkości b
i f wyra¿ą siê nastêpującymi wzorami:
, a wielkości b
i f wyra¿ą siê nastêpującymi wzorami:
![]()
![]() .
.
Oczywiście, gdybyśmy chcieli byæ bardziej dok³adni, to powinniśmy udowodniæ, ¿e tak zdefiniowana p³aszczyzna g³ówna jest tak¿e p³aszczyzną g³ówną w sensie poprzednich definicji (w duchu modelu Möbiusa-Gaussa), czyli, ¿e w obu p³aszczyznach g³ównych skupiona jest ca³a moc soczewki grubej itd. ¯eby tego dokonaæ, nale¿a³oby pokazaæ (u¿ywając np podejścia macierzowego) równowa¿nośæ soczewki grubej i modelu M-G (czyli równośæ odpowiednich macierzy). Oczywiście nale¿a³oby wziąæ pod uwagê, ¿e grubośæ warstwy pomiêdzy p³aszczyznami g³ównymi w modelu M-G powinna byæ zredukowana o wielkośæ
![]() ,
,
opisującą odleg³ośæ miêdzy punktem wierzcho³kowym V2 i punktem przeciêcia osi optycznej p³aszczyzną g³ówną H2 i o analogiczną wielkośæ
![]()
obliczoną dla przedniej strony soczewki grubej, opisującą odleg³ośæ pomiêdzy punktem wierzcho³kowym V1 i punktem przeciêcia osi optycznej p³aszczyzną g³ówną H1.
Oba powy¿sze wyra¿enia poprawnie redukują siê do zera dla grubości d zmierzającej do zera. Przez P oznaczyliśmy moc ca³kowitą soczewki grubej, która wyrazi siê nastêpującym wzorem:
![]() ,
,
gdzie d jest grubością soczewki a P1 i P2 mocami optycznymi jej obu powierzchni. Warto zwróciæ uwagê, ¿e wyra¿enie to, tak jak nale¿a³oby oczekiwaæ, redukuje siê do sumy moc optycznych obu powierzchni gdy d zmierza do zera, wynik, który wcześniej otrzymaliśmy w sposób ścis³y dla soczewki cienkiej stosując zasadê Fermata.
Jak wynika z przedstawionych wy¿ej obliczeñ sta³e Gaussa dla soczewki grubej opisane bêdą nastêpującymi wyra¿eniami (sta³ą Gaussa d oznaczyliśmy dG dla odró¿nienia od grubości soczewki d):
![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
,
gdzie z wielkością b , równą jak siê okazuje parametrowi Gaussa c, mieliśmy przed chwilą do czynienia; jak pamiêtamy, wyra¿enie (b -1)x, gdzie x to po³o¿enie ogniska liczone od p³aszczyzny ³amiącej, określa³o po³o¿enie p³aszczyzny g³ównej po stronie obrazu (analogicznie wyra¿enie (a -1)x określa po³o¿enie p³aszczyzny g³ównej po stronie przedmiotu). Oczywiście przyjêliśmy tutaj, podobnie jak w obliczeniach macierzowych dla soczewki grubej, ¿e rozpatrywany uk³ad optyczny to soczewka gruba zrobiona z materia³u o wspó³czynniku za³amania n i znajdująca siê w powietrzu. Z innych parametrów wystêpujących w powy¿szych relacjach sta³a Gaussa a odpowiada ca³kowitej mocy soczewki, zaś sta³a Gaussa dG wią¿e siê z grubością zredukowaną soczewki ze znakiem minus (wielka szkoda, a¿ trudno w to uwierzyæ, mo¿e siê jednak gdzieś pomyliliśmy? albo, byæ mo¿e, definicja sta³ych Gaussa, wziêta z Meyera-Arendta nie jest prawid³owa co do znaku tej ostatniej sta³ej).
Rozpatrzymy teraz dzia³anie soczewki grubej; spróbujemy mianowicie znale¼æ postaæ równania soczewkowego wią¿ącego odleg³ośæ przedmiotu s0 i obrazu s1. W tym celu rozpatrzymy dok³adniej sytuacjê przedstawioną na rys. 28, gdzie S i P są punktami sprzê¿onymi (punkt P jest obrazem punktu S) przez soczewkê grubą.

Rys. 28. Ogniskujące dzia³anie soczewki grubej. Rozbie¿na wiązka rozchodząca siê ze ¼ród³a S zostaje przez soczewkê skupiona w punkcie P. Odleg³ości przedmiotu od pierwszej p³aszczyzny ³amiącej i pierwszej p³aszczyzny g³ównej wynoszą x i s0; te same wielkości dla obrazu wynoszą odpowiednio y i s1.
Macierz soczewki grubej przedstawimy w nastêpujący wygodny sposób uwzglêdniając naszą wcześniejszą dyskusjê sta³ych a , b i P (d jest grubością soczewki, czyli odleg³ością pomiêdzy powierzchniami ³amiącymi, tak jak poprzednio):
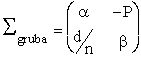 .
.
Jak wynika z rysunku 28, macierz tê nale¿y teraz pomno¿yæ przez macierze translacji od przedmiotu do soczewki (odleg³ośæ przedmiotowa x) i od soczewki do obrazu (odleg³ośæ obrazowa y):
 ,
,
po przemno¿eniu otrzymujemy macierz ca³ego uk³adu:
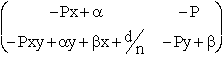 .
.
Zastanówmy siê teraz, jakie warunki powinny spe³niaæ elementy tej macierzy, ¿eby uk³ad rzeczywiście transformowa³ punkt na punkt (innymi s³owy, ¿eby punkty w x i y by³y sprzê¿one)? Wyobra¼my sobie, ¿e pierwszy element w drugim wierszu jest równy zero. Co to fizycznie oznacza? Pamiêtamy, ¿e drugi wiersz s³u¿y do obliczania wysokości h promienia w punkcie P (czyli y od p³aszczyzny ³amiącej), a jego pierwszy element daje wk³ad do tego h pochodzący od kąta g promienia wejściowego (w punkcie S). Jeśli ten w³aśnie element bêdzie równy zero to niezale¿nie od kąta g wysokośæ h promienia wyjściowego bêdzie taka sama co oznacza, ¿e ca³a rozbie¿na wiązka promieni wychodząca z punktu S w x, skupi siê w punkcie P o wysokości h w y. (Tak naprawdê to niedawno o tym mówiliśmy, popatrzcie na przypadek 1 w poprzednim wyk³adzie nr 6). A wiêc:
![]()
Chocia¿ to równanie wygląda na pierwszy rzut oka obiecująco, nic prostego (tzn szukanego równania soczewkowego, 1/x+1/y = 1/f) z niego nie otrzymamy. Trzy pierwsze wyrazy dają co prawda równanie wią¿ące x, y i f w szukanej prostej postaci, ale wielkośæ d/xy (z wyjątkiem bardzo szczególnych sytuacji) nigdy nie bêdzie równa zeru dla soczewki grubej, dla której nie mo¿emy (i nie chcemy) pominąæ grubości d.
Wprowad¼my zatem wspó³rzêdne s0 i s1

bo w takich przecie¿ wspó³rzêdnych powinno nam wyjśæ równanie soczewkowe. Po podstawieniu otrzymujemy:
![]() .
.
Prawa strona tego równania, o ile strona lewa bêdzie równa zeru dla wszystkich wartości s0 i s1 (na co jest szansa, bo strona ta zale¿y wy³ącznie od sta³ych parametrów a , b , f i d/n) da nam poszukiwane równanie soczewkowe, dzieląc bowiem przez iloczyn s0s1 i przenosząc podwójny wyraz na przeciwną stronê otrzymamy:
 .
.
A zatem pozostaje nam udowodniæ, ¿e ![]()
![]() ;
; ![]() ;
; ![]()
Podstawiając powy¿sze definicje do wyra¿enia (1-a b )/P otrzymamy:
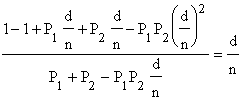
co oczywiście oznacza, ¿e ca³e wyra¿enie (1-a b )/P-d/n jest równe zero i koñczy ca³y dowód. Zaś dowód ten koñczy naszą prezentacjê zastosowañ rachunku macierzowego w optyce geometrycznej i, zgodnie z planem, ca³ej optyki geometrycznej.
Uwagi koñcowe
Pozosta³o bardzo wiele zagadnieñ optyki geometrycznej, które moglibyśmy rozpatrywaæ w oparciu o ca³kiem mocny formalizm macierzowy, którego siê nauczyliśmy. Tym z Was, którzy znają jêzyk rosyjski (przynajmniej na tyle, ¿eby czytaæ) polecam bardzo ciekawą ksią¿kê, jest to stare (i zapewne nielegalne) t³umaczenie ksią¿ki A. Gerrarda i J.M. Burcha, Introduction to Matrix Methods in Optics, rosyjski tytu³ Wwiedienje w matricznuju optiku, Mir, Moskwa 1978. Jest jeden egzemplarz tej ksią¿ki w bibliotece IF UMK. Gdyby kiedykolwiek uda³o Wam siê zobaczyæ tê ksią¼kê np w antykwariacie to warto kupiæ, nie powinna byæ zbyt droga, te ksią¿ki nie tak dawno temu by³y naprawdê bardzo tanie.
Istnieje tak¿e wiele zagadnieñ, które nie wymagają koniecznie znajomości rachunku macierzowego, niektóre z nich są bardzo ciekawe i wa¿ne. Mimo tego, ze wzglêdu na zakres materia³u, który powinien znale¿æ siê w tym wyk³adzie, pora zakoñczyæ ten specyficzny i historycznie bardzo obcią¿ony dzia³ optyki, zwany optyką geometryczną i przejśæ do nastêpnego, równie co prawda historycznie obcią¿onego, czyli do optyki falowej.