WYKŁAD 6
1.6 Rachunek macierzowy
Zastosowanie rachunku macierzowego do analizy złożonych układów optycznych
Dokładne metody analityczne a także wszelkiego rodzaju metody przybliżone były bardzo ważne dawniej; kiedy nie było komputerów, także później, kiedy dostêpne komputery nie posiadały potrzebnej mocy obliczeniowej. Dzisiaj nadal wysoko cenimy takie metody ale, ze wzglêdu na olbrzymi postêp w technikach i technologii komputerowej, na czoło wysunął siê zupełnie inny, choæ także bardzo ważny (może nawet waźniejszy) powód; analiza układu fizycznego i jego modelowanie, uwzglêdniające stopieñ ważności różnych czynników określających ten układ, jego działanie czy też ewolucjê umożliwia nam bowiem głêbsze fizyczne zrozumienie tego układu. To z kolei potrzebne jest do wyobrażenia sobie, jak działałby układ trochê zmodyfikowany czy zmieniony, po uwzglêdnieniu dodatkowego czynnika itd. Myślenie w kategoriach modelowych, polegające na tym, że najpierw upraszczamy, potem dopiero uwzglêdniamy kolejne dokładniejsze przybliżenia (oczywiście tylko takie, które w danej sytuacji są niezbêdne dla zrozumienia układu ale nic ponad to) to dla wielu fizyków istota myślenia fizycznego, podstawowa metoda fizyki.
Poprzednio przedstawiliśmy Wam model układu optycznego, w którym korzystaliśmy z przybliżonych pojêæ takich jak płaszczyzny główne, ogniskowe, punkty kardynalne itd. Model ten umożliwiał nam narysowanie (wytyczenie) torów przebiegających przez układ promieni świetlnych a także obliczenie pewnych ważnych wielkości charakteryzujących obraz jak powiêkszenie poprzeczne i podłużne, położenie itd. Obecnie przedstawimy podejście, które umoźliwia nam obliczenie przebiegu toru dowolnego promienia świetlnego przez układ optyczny, zawierający bardzo dużą liczbê elementów (soczewek) o dowolnych grubościach, współczynnikach załamania itd.

Rys. 22. "Położenie" promienia w układzie optycznym o osi optycznej SOP określimy przy pomocy dwóch współrzêdnych, "wysokości" h i kąta g . O ile współczynnik załamania po obu stronach powierzchni AO jest taki sam, wartośæ kąta g nie zmienia siê i bêdzie taka sama po obu stronach powierzchni AO.
Opis przebiegu promienia świetlnego w układzie optycznym wymaga przede wszystkim wprowadzenia charakterystycznych dla niego "współrzêdnych", które opisywaæ bêdą jego w tym układzie "położenie". Jak pokazano na rys. 22, promieñ w układzie o osi optycznej SOP, przecinający pewną powierzchniê w punkcie A, może byæ jednoznacznie opisany przez podanie dwóch liczb; kąta g , który ten promieñ tworzy z osią optyczną i odległości od osi optycznej, h. Tak wiêc każdemu promieniowi możemy przypisaæ jednokolumnową macierz o dwóch wierszach (1x2):
![]() ,
,
gdzie n jest współczynnikiem załamania (potrzeba wprowadzenia w tym miejscu współczynnika załamania stanie siê jasna trochê później). Dla ułatwienia bêdziemy czasem pisaæ po prostu (n× g ,h) ale bêdziemy pamiêtali, że promieñ przedstawiamy przy pomocy macierzy jednokolumnowej i dwuwierszowej.
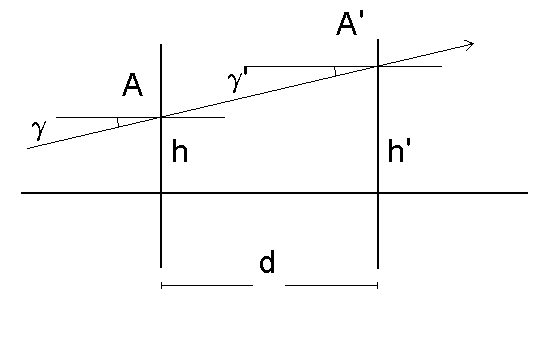
Rys. 23. Po przejściu jednorodnej warstwy o grubości d i współczynniku załamania n, promieñ (g ,h) transformuje siê w promieñ (g ,h).
Oczywiście wiemy, że przejście promienia np przez granicê ośrodków o różnych współczynnikach załamania zmieni kąt g ; z drugiej strony tylko dla g = 0 mielibyśmy zawsze to samo h, tak wiêc dużo może siê zmieniaæ i powinniśmy dokładniej zbadaæ, co siê dzieje z macierzą reprezentującą promieñ w różnych sytuacjach. Zaczniemy od najprostszej, zbadamy, co siê dzieje z macierzą x po przejściu jednorodnej warstwy o grubości d i współczynniku załamania n (rys. 23). Symbolicznie możemy, korzystając z zapisu macierzowego, przedstawiæ tê transformacjê w nastêpujący sposób:
![]() ,
,
gdzie x oznacza macierz reprezentującą promieñ wchodzący do warstwy d, x macierz promienia z niej wychodzącego, natomiast  (d,n) oznacza macierz reprezentującą warstwê ośrodka o współczynniku załamania n (ponieważ oprócz prostego przesuniêcia nic innego z promieniem siê w tym przypadku nie dzieje, macierz tê nazywamy macierzą translacji). Jak pokazano na rys. 23, po przejściu warstwy promieñ bêdzie opisany współrzêdnymi g i h, przy czym g = g , h = h + d× tgg . W przybliżeniu promieni przyosiowych tgg @ g , a wiêc h = h + d× g i:
![]() .
.
Korzystając z reguł mnożenia macierzy można łatwo odgadnąæ (jak ktoś chce, może to sobie formalnie wyliczyæ, pisząc odpowiednie dwa równania):
![]() .
.
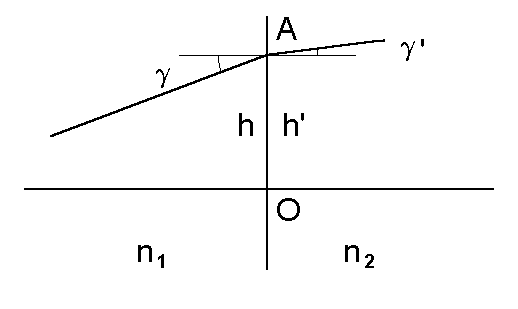
Rys. 24. Transformacja promienia na granicy dwóch ośrodków o różnych współczynnikach załamania n1 i n2.
Nastêpny przypadek, który rozpatrzymy to transformacja macierzy promienia x na granicy dwóch ośrodków o różnych współczynnikach załamania n1 i n2. Jak widaæ na rys. 24 wysokośæ h i h są tym razem jednakowe, h = h, natomiast zmianie ulegnie kąt g . Z prawa Snella w przybliżeniu małych kątów mamy n1× g = n2× g a wiêc:
![]() .
.
Z drugiej strony:
![]()
i widaæ teraz korzyści z zastosowania mnożnika przy kącie g w postaci współczynnika załamania; macierz załamania X (n1, n2) przyjmie bowiem szczególnie prostą postaæ:
![]() .
.
Nastêpny szczególny przypadek, który rozważymy to przejście promienia świetlnego przez łamiącą powierzchniê sferyczną oddzielającą ośrodki o współczynnikach załamania n1 i n2 (rys. 25).

Rys. 25. Transformacja macierzy promienia świetlnego na granicy dwóch ośrodków o współczynnikach załamania n1 i n2. Powierzchnia ma kształt sferyczny, ze środkiem w punkcie O i promieniu krzywizny AO równym R. Promieñ padający SA przechodzi w promieñ AP; wysokośæ h jest zachowana, a kąt g ulega zmianie zgodnie z prawem Snella.
Z prawa Snella mamy:
![]() ,
,
przy czym
![]()
![]() ,
,
a kąt d w przybliżeniu promieni przyosiowych (a zatem małych kątów)
![]() .
.
Ostatecznie mamy zatem:
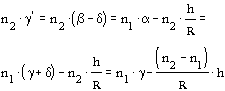
a także mamy h = h. Ponieważ (n2 -n1)/R jest mocą optyczną sferycznej powierzchni łamiącej, P, wiêc macierz charakteryzująca tê powierzchniê, S (R) przyjmie postaæ:
![]() .
.
Mając do dyspozycji macierze reprezentujące różne elementy układu optycznego, możemy obliczyæ przebieg promienia świetlnego przez cały układ, mnoźąc kolejno macierz promienia x przez odpowiednie macierze elementów układu. Inny sposób postêpowania, znacznie bardziej ogólny, polega na obliczeniu macierzy reprezentującej cały układ. Nastêpnie, zmieniając odpowiednio macierz promienia i mnożąc tê macierz przez macierz całego układu możemy otrzymaæ cały zbiór promieni wychodzących z układu. Dla przykładu obliczymy teraz macierz charakteryzującą soczewkê grubą o grubości d i dwóch cylindrycznych powierzchniach łamiących o promieniach krzywizny R1 i R2 (zmieniając znak promieni krzywizny bêdziemy mogli uwzglêdniæ różne soczewki, dwuwypukłe, dwuwklêsłe, płasko - wypukłe itd). Macierz soczewki grubej (oznaczymy ją W (R1,d,R2)) powinna zawieraæ macierz załamania pierwszej powierzchni łamiącej S 1(R1), nastêpnie macierz translacji  (d) i w koñcu macierz drugiej powierzchni łamiącej S 2(R2). A zatem, pisząc macierze składowe w odpowiedniej kolejności (ta macierz, która "wcześniej" działa na promieñ, wystêpuje po prawej stronie) otrzymamy: W (R1,d,R2) = S 2(R2)× Â (d)× S 1(R1). Podstawiając mamy:
 ,
,
gdzie cztery elementy macierzy układu W nazywamy stałymi Gaussa a, b, c i d układu optycznego, P1 i P2 są mocami optycznymi powierzchni łamiących soczewki grubej, n2 współczynnikiem załamania materiału soczewki a d jej grubością (tak siê nieprzyjemnie złożyło, że mamy tutaj dwie stałe d, które są sobie na dodatek prawie równe, z dokładnością do współczynnika załamania, ciekawe, czy to przypadek?). Szczegóły dalszych obliczeñ (macierzy soczewki i coś jeszcze, żeby pokazaæ, że takie macierze do czegoś siê mogą przydaæ) przedstawimy w nastêpnym wykładzie. Już teraz jednak warto powiedzieæ, że obliczenia te (i niektóre dawniejsze) pozwalają powiązaæ ważne parametry, charakteryzujące soczewkê sferyczną, takie jak ogniskowa soczewki, jej całkowita moc optyczna, odległości płaszczyzn głównych od wierzchołków, moce optyczne powierzchni łamiących z parametrami geometrycznymi jak grubośæ, promienie krzywizny powierzchni łamiących i współczynnik załamania.
Macierz złożonego układu optycznego z translacjami - przypadki specjalne
Rozważymy teraz przypadek bliżej niesprecyzowanego układu optycznego, przedstawionego na rys. 26 i składającego siê z pewnej liczby powierzchni łamiących. Do macierzy U tego układu dołączamy macierze translacji, macierz T1, od pewnej płaszczyzny S1 do układu optycznego i potem macierz T2, od układu optycznego do płaszczyzny S2 tak jak pokazuje rys. 26.
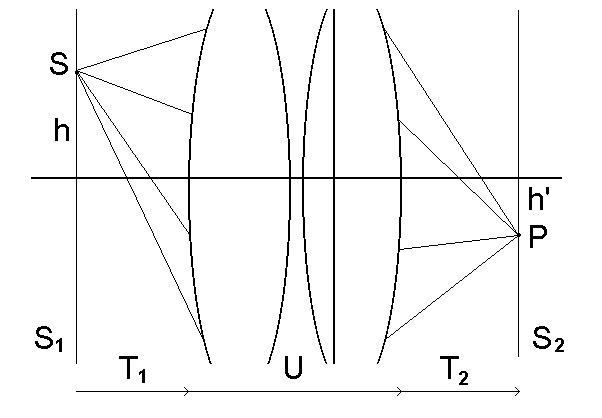
Rys. 26. Złożony układ optyczny. Do układu dołączamy dwie translacje, T1, od płaszczyzny S1 do układu i T2, od układu do płaszczyzny S2. W przypadku pokazanym na rysunku układ odwzorowuje punkt S w punkt P (punkty S i P są sprzêżone).
Macierz UC, która bêdzie równa:
![]()
wyrazimy poprzez pewne stałe A, B, C i D (w nastêpnym wykładzie znajdziemy wartośæ tych stałych dla przypadku soczewki grubej).
Na rys. 26 pokazany jest pewien specjalny przypadek, w którym układ odwzorowuje punkt S na punkt P. Tak nie zawsze musi byæ, załóźmy na razie, źe punkt P został wyznaczony przez przeciêcie płaszczyzny S2 pewnym (byæ moźe jedynym) promieniem wychodzącym z punktu S i przechodzącym przez układ optyczny (wiêkszośæ promieni, wchodzących do układu musi z niego wyjśæ, to ma byæ w koñcu układ optyczny a nie czarna dziura). Dla tego szczególnego promienia bêdziemy oczywiście mieli nastêpującą relacjê:
![]() ,
,
zatem
![]() ,
,
i możliwe są różne szczególne przypadki. Pokażemy, że jeden z nich odpowiada sytuacji z rys. 26 (tzn, źe istnieją punkty sprzêźone).
Przypadek 1. C = 0. Mamy zatem:
h= 0g + Dh = Dh
i wszystkie promienie (a nie jakiś jeden specjalny) wychodzące z S bêdą na płaszczyźnie S2 posiadały tê samą wartośæ h, niezależnie od początkowej wartości g i koñcowej g . Zatem narzucenie na układ warunku C = 0 spowoduje, że układ bêdzie odwzorowywał punkt S na punkt P lub ogólniej, obraz przedmiotu umieszczonego w płaszczyźnie S1 bêdzie znajdował siê w płaszczyźnie S2. Parametr D natomiast odegra rolê powiêkszenia poprzecznego (jak ktoś chce, to może wykorzystaæ tê informacjê i gotowe wzory z nastêpnego wykładu i zająæ siê problemem powiêkszenia poprzecznego dla soczewki grubej). Przedyskutowane wyżej konsekwencje zerowania siê C wykorzystamy w nastêpnym wykładzie, w którym udowodnimy, źe postaæ równania soczewkowego dla soczewki grubej jest taka sama jak dla soczewki cienkiej o ile zdefiniujemy odpowiednio odległości przedmiotową i obrazową.
Przypadek 2. Rozpatrzymy nastêpny przypadek, A = 0. Mamy wtedy:
g = 0g + Bh
co oznacza, że niezależnie od wartości kąta g kąt g przyjmie jedną wartośæ zależną od parametru B i odległości punktu S od osi optycznej (czyli wiązka rozbieżna emitowana z S transformuje siê w wiązkê równoległą). Zatem płaszczyzna S1 bêdzie pierwszą płaszczyzną ogniskową a odległośæ x przyjmie wartośæ równą wartości ogniskowej przedmiotowej układu pomniejszonej o odległośæ punktu wierzchołkowego od płaszczyzny głównej.
Przypadek 3. Niech B = 0. Wówczas:
g = Ag + 0h .
W szczególności wiązka równoległa padająca na układ wyjdzie z niego jako wiązka równoległa przy czym powiêkszenie kątowe układu bêdzie zależało od wartości parametru A. Układy takie mają znaczenie dla przyrządów optycznych (pewnie w astronomii?).
Przypadek 4. Ostatni szczególny przypadek to D = 0. Mamy wówczas:
h = Cg + 0h = Cg ,
a wiêc, o ile wiązka padająca na układ od strony płaszczyzny S1 jest równoległa (czyli wszystkie kąty g są takie same) to wiązka wychodząca bêdzie skupiona w jednym punkcie o wysokości h zależnej od kąta g i wartości stałej C. Oznacza to ni mniej ni wiêcej, iż płaszczyzna S2 jest drugą płaszczyzną ogniskową, a odległośæ y tej płaszczyzny od układu jest równa ogniskowej obrazowej układu pomniejszonej o odległośæ punktu wierzchołkowego od płaszczyzny głównej, podobnie jak dla przypadku 2.