
WYKŁAD 5
1.5 Układy sferyczne
Układy sferyczne - odwzorowanie obiektów trójwymiarowych
Do tej pory rozważaliśmy odwzorowanie punktowego źródła światła S przez sferyczne układy optyczne, przy tym ograniczyliśmy siê do punktów leżących na osi optycznej. Realne obiekty są jednak trójwymiarowe; możemy oczywiście wyobraziæ je sobie w postaci rozciągłego zbioru źródeł punktowych, ale w ogólności muszą znależæ siê w tym zbiorze punkty nie leżące na osi optycznej.

Rys. 16. Pojedyncza powierzchnia sferyczna. Odwzorowanie punktów nie leżących na osi optycznej. "Prawdziwym" obrazem punktu A jest punkt A, bardzo blisko którego leży jednak punkt A. W układzie sferycznym obie proste, BOB i ABA mogą byæ osiami optycznymi, wybieramy jednak prostą BOB. Punkt O jest środkiem krzywizny powierzchni załamującej.
Na rysunku 16 przedstawiamy "obiekt", który składa siê z dwóch punktów, A i B, przy tym odcinek AB jest prostopadły do prostej wyznaczonej przez punkty BOB. Obrazy punktów B i A bêdą leżały w odległościach wyznaczonych przez równanie pojedynczej powierzchni, na prostych AO i BO; przyjmijmy, że bêdą to punkty B i A. Chcemy ustaliæ, czy punkt A jest przesuniêty w stronê "do" czy "od" powierzchni załamującej wzglêdem punktu A (odcinek AB jest prostopadły do prostej BOB). W tym celu róniczkujemy równanie pojedynczej powierzchni i otrzymujemy

zatem znaki przyrostów D s0 i D s1 są przeciwne. Oznacza to, że z s0A > s0B wynika s1A < s1B i punkt A jest przesuniêty w lewo w stosunku do punktu A. Wielkośæ tego przesuniêcia bêdzie jednak, w przybliżeniu optyki gaussowskiej, bardzo mała, rzêdu h2 /2s0 (dokładniej ~ h2 s12 /2s03) gdzie h jest długością odcinka AB. Możemy zatem przyjąæ, że odwzorowanie punktów leżących blisko osi optycznej, zachodzi tak, że odcinki prostopadłe do osi optycznej są nadal prostopadłe do tej osi po transformacji przez jedną (a wiêc także przez dwie) powierzchnie sferyczne.
W szczególności dla nieskoñczenie daleko położonego przedmiotu (s0 = ¥ ) każdemu punktowi przedmiotu odpowiadaæ bêdzie wiązka równoległa o innym kącie nachylenia do osi optycznej. Jak pokazuje rys. 17, wiązka taka, po przejściu układu optycznego, skupiona zostanie w odpowiednim punkcie leżącym w tzw płaszczyźnie ogniskowej, prostopadłej do osi optycznej i przechodzącej przez ognisko obrazowe układu optycznego (w szczególności wiązka równoległa do osi optycznej zostanie skupiona w ognisku).
Do znalezienia obrazu punktu S leżącego na osi optycznej w przestrzeni przedmiotowej wystarczało zastosowanie równania soczewkowego (plus informacja, że obraz także leży na osi optycznej). Rozpatrując "obiekt" BA (rys. 16) wprowadziliśmy prostą AO aby zlokalizowaæ obraz punktu A, nie leżącego na osi optycznej BO.

Rys. 17. Wiązki równoległe o różnym kącie nachylenia do osi optycznej są ogniskowane w różnych punktach leżących w płaszczyźnie ogniskowej przechodzącej przez ognisko obrazowe Fo i prostopadłej do osi optycznej. Odległośæ PFo »afO.
W ogólności znacznie łatwiej jest posługiwaæ siê techniką wytyczania biegu promieni. Technika ta korzysta z faktu, że każdy punkt w przestrzeni obrazowej powstaje w wyniku zogniskowania wszystkich promieni wychodzących ze sprzêżonego punktu w przestrzeni przedmiotowej i trafiających do układu optycznego. Zatem dla ustalenia położenia obrazu wystarczy wyznaczenie biegu dwóch dowolnie wybranych promieni z wiązki padającej na układ. Meyer - Arendt opisuje interesujące metody wytyczania biegu dowolnego promienia, metodê promienia równoległego i metodê promienia nachylonego (pomimo nazw sugerujących coś innego, są to metody umożliwiające wytyczenie dowolnego promienia) korzystające z prostych konstrukcji geometrycznych (Meyer - Arendt, str. 56-63). Najłatwiej jednak jest szukaæ obrazu przez wykorzystanie nie dowolnych ale wybranych promieni o specjalnych własnościach umoźliwiających ich szybkie wytyczenie. Technikê, tê zapoczątkował swoimi pracami Robert Smith w 1738 roku.
Trzy promienie, których bieg w układzie optycznym można latwo wytyczyæ to:

Rys. 18. Wyznaczanie położenia obrazu wytworzonego przez soczewkê cienką przy pomocy wyznaczania biegu promieni równoległego (1), głównego (2) i ogniskowego (3)
Wytyczenie biegu każdych dwóch spośród trzech wyliczonych wyżej promieni do punktu ich przeciêcia (w przypadku obrazu pozornego należy przedłużyæ promienie "wstecz"), wystarcza do znalezienia obrazu dowolnego punktu; zatem po uwzglêdnieniu dostatecznej liczby punktów, także dowolnego trójwymiarowego przedmiotu. Na rys. 18 obraz P2 punktu S2 stanowiącego "czubek" strzałki S1S2 utworzony przez soczewkê cienką o ogniskowej f, ogniskach FP i OF, został wyznaczony jako punkt przeciêcia trzech wybranych promieni: równoległego (1), głównego (2) i ogniskowego (3). Obrazem punktu S1 jest punkt P1. W ten sposób łatwo znajdujemy rzeczywisty obraz P1P2 przedmiotu S1S2, którym jest strzałka. Obraz jest rzeczywisty, odwrócony i pomniejszony co wynika z faktu, że odległośæ s0 jest wiêksza od 2f (z równania soczewkowego można wówczas znaleźæ, źe f £ s1 £ 2f) a o powiêkszeniu za chwilê dokładniej.
Powiêkszenie poprzeczne i podłużne obrazu utworzonego przez soczewkê cienką
Powiêkszenie poprzeczne MT obrazu definiujemy jako:
![]() ,
,
z porównania trójkątów S1S2O i P1P2O a także zgodnie z ogólnie przyjêtą konwencją, że odległości powyżej osi optycznej liczymy jako dodatnie, a poniżej jako ujemne. Tak wiêc dla obrazu rzeczywistego MT bêdzie zawsze ujemne (s1 i s0 dodatnie) a wartośæ bezwzglêdna może byæ zarówno wiêksza jak mniejsza od 1. Porównując trójkąty S1S2FP i OBFP a także P1P2FO i AOFO mamy:
![]() ,
,
gdzie x1 =P1FO i x0 = S1FP są odległościami przedmiotu i obrazu od odpowiednich ognisk (są to odległości newtonowskie, które wprowadziliśmy poprzednio).
Powiêkszenie podłużne obrazu ML definiujemy jako:
![]() lub
lub ![]() .
.
Ponieważ x0x1 = f2 (równanie Newtona) wiêc łatwiej chyba wykorzystaæ drugą z powyższych, całkowicie zresztą równoważnych definicji. Różniczkując otrzymujemy:
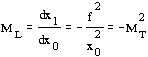 .
.
Oznacza to, że po pierwsze, "ubytkom" x0 towarzyszą "przyrosty" x1 (strzałka skierowana do soczewki zostanie odwzorowana w strzałkê skierowaną od soczewki), po drugie, oba powiêkszenia są różne; można wiêc oczekiwaæ dystorsji obrazu, szczególnie wtedy, gdy oczekujemy dużych powiêkszeñ lub pomniejszeñ (jeśli MT » 1 to także ML » 1).
Układy złożone i soczewki grube - koncepcja płaszczyzn głównych i punktów kardynalnych
Rozpatrując układy złożone i soczewki grube przyjmiemy za Möbiusem i Gaussem, że dowolny układ optyczny opisaæ moźna przy pomocy modelu, w którym zakłada siê, że załamanie promieni wiązki światła w układzie zachodzi tylko i wyłącznie w dwóch tzw płaszczyznach głównych prostopadłych do osi optycznej i zlokalizowanych na ogół wewnątrz układu (soczewki). Oznacza to, że w płaszczyznach tych skupiona jest całkowita moc optyczna układu. Dla cienkiej soczewki obie płaszczyzny główne pokrywają siê, a ich moc optyczna, jak pokazaliśmy wcześniej, jest po prostu równa sumie mocy optycznych obu powierzchni załamujących tworzących soczewkê. Dla soczewek nieco grubszych, dla których suma mocy optycznych obu powierzchni załamujących różni siê trochê, choæ niezbyt znacznie, od całkowitej mocy soczewki, możemy spodziewaæ siê, że płaszczyzny główne bêdą znajdowały siê w pobliżu zewnêtrznych powierzchni soczewki. Punkty przeciêcia płaszczyzn głównych z osią optyczną, tzw punkty główne, powinny zatem byæ zlokalizowane niezbyt daleko od punktów wierzchołkowych (V1 na rys. 19).

Rys. 19. Rzeczywisty (linia przerywana) i zgodny z modelem Möbiusa-Gaussa przebieg promieni tworzących rozbieżną wiązkê światła rozchodzącego siê z ogniska FP soczewki grubej. W rzeczywistości załamanie nastêpuje na obu powierzchniach sferycznych; zgodnie z modelem, wyłącznie na płaszczyznach głównych. Na rysunku pokazano pierwszą płaszczyznê główną, której przeciêcie z osią optyczną wyznacza pierwszy punkt główny H1.
Na rys. 19 pokazujemy geometryczny sposób wyznaczenia pierwszej płaszczyzny głównej układu skupiającego wykorzystujący własnośæ ogniskowania (wiązka rozbieżna rozchodząca siê z ogniska FP wyjdzie z układu w postaci wiązki równoległej), a także wykorzystujący własności płaszczyzny głównej. Skoncentrowanie mocy optycznej w płaszczyznach głównych oznacza przecież, że załamanie nastêpuje wyłącznie na tych właśnie płaszczyznach. Zatem przedłużenie promieni padających na układ i wychodzących z układu i ustalenie punktów przeciêcia umożliwia wyznaczenie położenia pierwszej płaszczyzny głównej. Podobnie wyznaczyæ można położenie drugiej płaszczyzny głównej wykorzystując drugie ognisko, FO (i wiązkê równoległą, padającą na układ). Jak pokazano na rysunku, ogniskową f mierzymy od płaszczyzny głównej do ogniska. Punkty główne, ogniska i tzw punkty wêzłowe, nazywane są punktami kardynalnymi. Na rysunku 20 przedstawiono sposób geometrycznego znajdowania punktów wêzłowych N1 i N2. Cechą charakterystyczną punktów wêzłowych jest to, że przechodzące przez nie promienie ulegają jedynie przesuniêciu równoległemu, nie ulegają natomiast załamaniu. Z równoległej wiązki padającej na układ optyczny pod pewnym kątem, tylko jeden promieñ (oznaczony jako 3), przechodzący przez pierwszy punkt wêzłowy N1, który po przejściu układu przyjmie kierunek równoległy do kierunku padania promienia 1 i jako promieñ 2 przetnie płaszczyznê ogniskową w punkcie P. Przeciêcie tego promienia z osią optyczną wyznacza drugi punkt wêzłowy N2. Położenie punktów wêzłowych jest ważne dla wytyczania biegu promieni; Meyer-Arendt opisuje pomiar położenia punktów wêzłowych przy pomocy tzw metody przesuwu wêzłowego (str. 66).
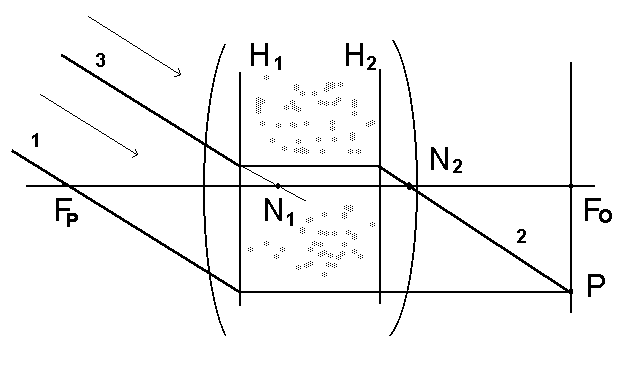
Rys. 20. Znajdowanie punktów wêzłowych. Promienie 1, 2 i 3 są równoległe, a przeciêcia promieni 3 i 2 z osią optyczną definiują punkty wêzłowe N1 i N2.
Własności ogniskujące złożonego układu kilku soczewek czy też pojedynczej soczewki grubej, mogą byæ opisane przy pomocy sześciu punktów kardynalnych: dwóch ognisk, dwóch punktów głównych i dwóch punktów wêzłowych. Punkty główne i ogniskowe wyznaczają także płaszczyzny główne i ogniskowe. Warto także pamiêtaæ (choæ nie bêdziemy tego tutaj dowodziæ), że punkty wêzłowe na ogół pokrywają siê z punktami głównymi. Jak pokazano na rys. 21, znajomośæ położenia punktów kardynalnych umoźliwia wytyczenie biegu promienia głównego, ogniskowego i równoległego, a wiêc znalezienie obrazu dowolnego punktu czy przedmiotu.
Warto jeszcze raz podkreśliæ, że przebieg promieni pokazany na rys. 21 (także na rysunkach poprzednich) w obszarze soczewki nie musi i raczej na ogół nie odpowiada przebiegowi promieni rzeczywistych. Wynika on z zastosowania przybliżonego modelu w ramach tzw optyki gaussowskiej.
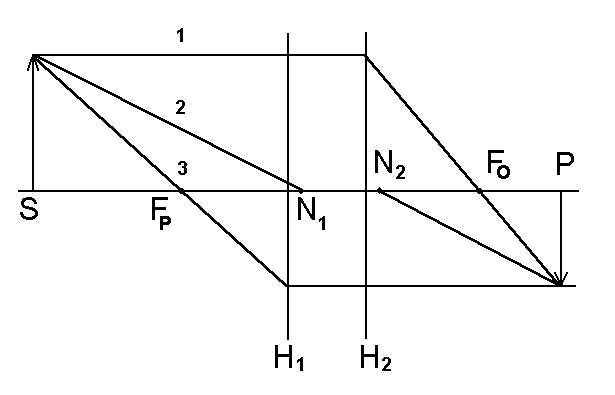
Rys. 21. Wytyczanie biegu promienia równoległego (1), głównego (2) i ogniskowego (3) przez soczewkê grubą lub złożony układ optyczny. FP i FO oznaczają ogniska, N1 i N2 punkty wêzłowe, a H1 i H2 - płaszczyzny główne.
Moc optyczna układu soczewek
Wyprowadzimy teraz wzór na moc optyczną układu dwóch soczwek cienkich rozsuniêtych na odległośæ d, wykorzystując podejście Meyera - Arendta (str. 102-103). Ze wzglêdu na możliwośæ zastąpienia takiego układu modelem przedstawionym na rys. 21, takim samym jak dla bardziej złożonego układu soczewek cienkich, grubych, lub pojedynczej soczewki grubej możemy, pod pewnymi warunkami, otrzymane wyrażenie traktowaæ bardziej ogólnie. W szczególności możemy założyæ, że układ dwóch soczewek cienkich o ogniskowych f1 i f2 odległych od siebie o d, jest równoważny soczewce grubej o grubości d, której powierzchnie łamiące charakteryzują siê takimi samymi ogniskowymi (czyli mocami optycznymi). Można rozsądnie założyæ, że oba takie układy bêdą nieźle reprezentowane przez taki sam model, przedstawiony na rys. 21. Powiêkszenie poprzeczne MT wyrazi siê wówczas nastêpującym wzorem:
![]() ,
,
gdzie s1,1, s0,1, s1,2, s0,2 oznaczają odpowiednio odległości obrazową i przedmiotową wzglêdem I i kolejno II soczewki (I i II powierzchni łamiącej), a s1 i s0 reprezentują odległości obrazową i przedmiotową liczoną wzglêdem punktów wêzłowych układu złożonego (czyli s1 = N2P, a s0 = N1S). Tak jak poprzednio mamy:
![]() ;
;
wykorzystamy także równanie Gaussa dla drugiej z dwóch cienkich soczewek tworzących rozpatrywany przez nas układ:
![]() skąd
skąd ![]() .
.
Ponieważ moc optyczna układu jest proporcjonalna do odwrotności jego ogniskowej chcemy wyliczyæ ogniskową f układu złożonego. Przyjmijmy zatem s0,1 = s0 = ¥ . Mamy wówczas: s1,1 = f1, s0,2 = -f1 + d i s1 = f. Zatem:
![]() .
.
dla układu dwóch soczewek cienkich rozsuniêtych na odległośæ d. W przypadku soczewki grubej musimy wziąæ pod uwagê współczynnik załamania ośrodka pomiêdzy powierzchniami łamiącymi, n. A wiêc:
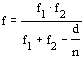 ,
,
albo, uwzglêdniając, że P = 1/f:
![]() ,
,
gdzie P jest mocą optyczną układu a P1 i P2 są mocami optycznymi zewnêtrznych powierzchni łamiących soczewki grubej. Tak jak należało oczekiwaæ wkład do całkowitej mocy optycznej soczewki, pochodzący od warstwy o grubości d jest do d proporcjonalny. W granicznym przypadku, gdy d ® 0, soczewka gruba przechodzi w cienką i P = P1 + P2., gdzie P1, P2 są mocami optycznymi powierzchni łamiących, tak jak należało oczekiwaæ (i jak otrzymaliśmy poprzednio w inny sposób dla soczewki cienkiej).
Łatwo także przewidzieæ (chociaż trochê trudniej to udowodniæ), że dla soczewki grubej w przybliżeniu promieni przyosiowych obowiązuje równanie soczewkowe:
![]() ,
,
gdzie, jeśli zastosujemy wyprowadzony wyżej wzór na ogniskową soczewki grubej i przypomnimy sobie wzory na ogniskowe powierzchni łamiących:
 .
.
We wzorze tym R1 i R2 to promienie krzywizny powierzchni zewnêtrznych soczewki grubej, n2 i n1 zaś to odpowiednio współczynniki załamania materiału soczewki i ośrodka.