WYKŁAD 3
1.3 Własności ogniskujące powierzchni kulistej w oparciu o zasadê Fermata
Do tej pory znajdowaliśmy dokładne wyrażenia opisujące powierzchnie układów optycznych działających w uproszczonych sytuacjach, takich mianowicie, gdy jeden punkt sprzêżony znajdował siê w nieskoñczoności a drugi w ognisku krzywej stożkowej albo odwrotnie (odwrócenie toru nie zmienia czasu przejścia promienia świetlnego po danym torze). Powierzchnie opisane krzywymi stożkowymi są jednak praktycznie trudniejsze do wykonania niż powierzchnie sferyczne. Wzglêdna łatwośæ wykonania powierzchni sferycznych wynika z ich specyficznych własności; dwa kawałki materiału, jeden o kształcie wklêsłym, drugiego wypukłym sferycznym o tej samej krzywiźnie bêdą do siebie idealnie przylegały. Zatem długotrwałe pocieranie o siebie we wszystkich możliwych kierunkach np wypukłego bloku szklanego i wklêsłej "formy"przedzielonych zawiesiną proszku polerskiego np w wodzie, bêdzie prowadziæ do zniewelowania wszelkich wypukłości na powierzchni obu kawałków materiałów, które bêdą coraz dokładnej "pasowały" do siebie. W ten sposób stosunkowo łatwo można zatem otrzymaæ wysokiej jakości powierzchnie sferyczne. Metoda taka była stosowana już na początku XVII wieku np przez Galileusza; nawet dziś, pomimo dostêpności sterowanych komputerowo obrabiarek umożliwiających otrzymanie dowolnej powierzchni, niski koszt prostej metody opisanej wyżej ułatwia masową tanią produkcjê i jest ona w powszechnym użyciu także dzisiaj. Tak wiêc warto zbadaæ własności ogniskujące prostych powierzchni sferycznych dla ogólnej sytuacji dowolnych punktów sprzêżonych nawet jeśli otrzymanie dobrej jakości odwzorowania może wymagaæ pewnych ograniczeñ np co do dopuszczalnych rozmiarów kątowych czy odległości od osi optycznej odwzorowywanych obiektów (przybliżenie promieni przyosiowych).
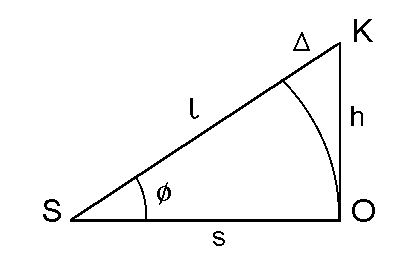
Rys. 12. Przybliżenie promieni przyosiowych. SO leży na osi optycznej zaś odcinek SK o długości l przedstawia promieñ przyosiowy. Dla małych kątów f SK = l = s + D @ s + h2/2s @ h2/2l.
Warunkiem dobrego odwzorowania punktu jest równośæ czasów przejścia (lub dróg optycznych) po różnych możliwych torach promienia świetlnego. Na rysunku 12 przedstawiamy dwa takie tory; SO (SO = s) i SK (SK = l). Ponieważ
![]()
a dla małych kątów f
![]()
wiêc
![]() .
.
W takim samym przybliżeniu mamy dalej f = sinf (sinf = h/l), lub f = tgf (tgf = h/s) zatem ostatecznie różnica dróg geometrycznych pomiêdzy dwoma promieniami wyniesie:
![]() .
.
Przybliżenie takie nazywamy przybliżeniem I rzêdu (w rozwiniêciu wziêliśmy wyrazy pierwszego rzêdu ze wzglêdu na f ), przybliżeniem gaussowskim albo przybliżeniem przyosiowym (paraksjalnym) a teoriê tworzenia obrazów w takim przybliżeniu nazywamy teorią promieni przyosiowych, teorią paraksjalną, lub teorią (optyką) gaussowską albo Gaussa (Gauss jako pierwszy rozpatrywał tworzenie siê obrazów w takim przybliżeniu).
Korzystając z wprowadzonego powyżej przybliżenia rozpatrzymy teraz odwzorowujące działanie pojedynczej powierzchni kulistej rozdzielającej dwa różne ośrodki, jeden optycznie rzadszy o współczynniku załamania n1 (np. powietrze) i drugi gêstszy o współczynniku załamania n2 (np. szkło), pokazanej na rysunku 13.
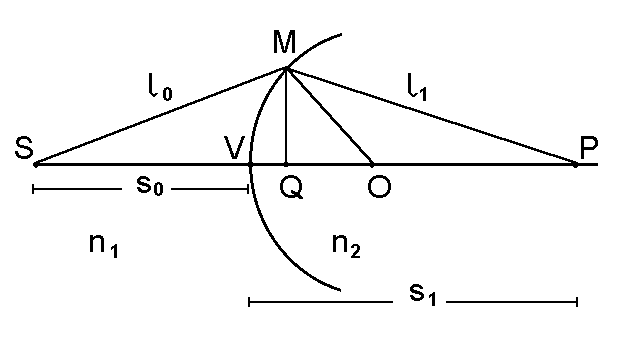
Rys. 13. Własności ogniskujące pojedynczej powierzchni kulistej. Punkt O jest środkiem a odcinek MO promieniem powierzchni kulistej oddzielającej dwa ośrodki o współczynnikach załamania n1 i n2. S i P są punktami sprzêżonymi leżącymi na osi optycznej, V i M to przeciêcia wybranych promieni z powierzchnią. s0 i s1 oznaczają odległości punktu S i jego obrazu od powierzchni (czyli od punktu V), l0 i l1 składają siê na geometryczną drogê promienia SMP.
Tak jak poprzednio, warunkiem dobrego odwzorowania punktu S na punkt P jest równośæ dróg optycznych (albo czasów przejśæ) dla wszystkich promieni. Rozpatrzymy dwa promienie; SVP i SMP. Długośæ drogi optycznej promienia SMP:
DDO1 = n1 l0 + n2 l1 ,
natomiast dla promienia SVP otrzymamy:
DDO2 = n1 s0 + n2 s1 .
Oznaczając VQ = D i MQ = h oraz przyjmując, że D < < s0, s1, otrzymamy zgodnie z rys. 12:
l0 = s0 + D + h2/2s0
l1 = s1 - D + h2/2s1 .
Stąd:
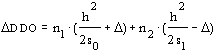 .
.
Z trójkąta MOQ w przybliżeniu przyosiowym mamy z kolei:
![]() ,
,
gdzie MO = R jest promieniem krzywizny, po podstawieniu do poprzedniego równania i położeniu D DDO = 0, ostatecznie otrzymujemy:
![]() ,
,
dobrze znane równanie (nazwiemy je na własny użytek "równaniem pojedynczej powierzchni"), wiążące ze sobą odległości od powierzchni ogniskującej przedmiotu s0 i obrazu s1.


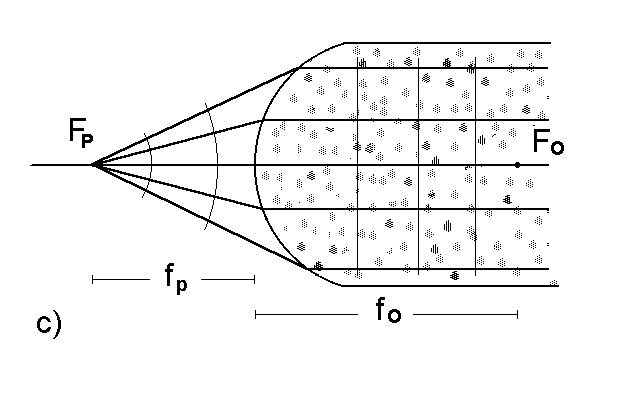

Rys. 14. Własności ogniskowania wypukłej powierzchni sferycznej. Warto zauważyæ, że we wszystkich pokazanych przypadkach zbieżnośæ wiązki po załamaniu na powierzchni rośnie; na rys. 14 a) wiązka równoległa transformuje siê w wiązkê zbieżną, przypadek b) jest najbardziej chyba oczywisty; wiązka rozbieżna transformuje siê w wiązkê zbieźną, c) to transformacja wiązki rozbieżnej w równoległą i w koñcu d) to transformacja wiązki silniej rozbieżnej w wiązkê słabiej rozbieżną.
Z równania pojedynczej powierzchni wynika, że suma dwóch wyrazów, pierwszego zależnego od s0 i drugiego od s1, jest stała. Wynika stąd, że jeśli przybliżamy przedmiot do powierzchni załamującej to jego obraz musi siê od niej oddalaæ. Dla s0 = R× n1 /(n2 - n1) drugi wyraz, n2 /s1, musi byæ równy zero, zatem s1 = ¥ . Oznacza to obraz w nieskoñczoności, czyli wiązkê równoległą po przejściu przez powierzchniê załamującą. Taka "specjalna" odległośæ s0 nazywa siê ogniskową przedmiotową (oznaczamy ją fP) albo pierwszą ogniskową a punkt ogniskiem przedmiotowym (FP), pierwotnym lub pierwszym. Przypadek taki pokazany jest na rys. 14 c). Niejako "odwrotny" przypadek, kiedy s0 = ¥ , a s1 = R× n2 /(n2 - n1) º fO jest pokazany na rys. 14 a). Interesująca sytuacja powstaje, gdy odległośæ przedmiotu od powierzchni s0 < fP. Jedyną szansą otrzymania równości w równaniu pojedynczej powierzchni jest wtedy by wyraz n2 /s1 był ujemny. Rzeczywiście ma to nawet sporo sensu, otrzymujemy bowiem w takiej sytuacji wiązkê rozbieżną a przedlużenie promieni prowadzi do punktu przeciêcia (czyli obrazu pozornego) po lewej czyli przeciwnej stronie układu optycznego (obraz rzeczywisty leży zawsze po prawej stronie układu (o ile przedmiot jest po lewej, ale taką właśnie przyjmujemy konwencjê) a odległośæ od powierzchni jest wtedy dodatnia.
Równanie pojedynczej powierzchni można wobec tego zapisaæ nastêpująco:
![]() ,
,
przy obowiązującej nastêpującej konwencji:
Reguła znaków
Warto zauważyæ, że wprowadzenie ujemnych odległości przedmiotowych i obrazowych prowadzi do poszerzenia przestrzeni przedmiotowej i obrazowej na całą przestrzeñ po obu stronach powierzchni.
Czêsto wprowadza siê dodatkowo pojêcia skolimowania, skolimowania zredukowanego (z uwzglêdnieniem współczynnika załamania) i mocy optycznej (patrz Meyer - Arendt, str. 43-44). Skolimowanie zredukowane wiązki przedmiotowej rozbieżnej definiujemy jako VP = n1 /s0, skolimowanie zredukowane wiązki obrazowej zbieżnej definiujemy jako VO = -n2 /s1 (a wiêc bêdzie ono ujemne dla obrazu rzeczywistego a dodatnie dla pozornego; innymi słowami ujemne dla wiązki zbieżnej i dodatnie dla rozbieżnej), a moc optyczną powierzchni załamującej (w 1/m, m-1, czyli w dioptriach) P = (n2 - n1) /R = n1 /fP = n2 /fO. Moc optyczna bêdzie zatem dodatnia dla powierzchni skupiających, a ujemna dla rozpraszających. Wymiarem skolimowania, podobnie jak mocy optycznej, bêdzie 1/m, m-1. Równanie pojedynczej powierzchni można wtedy zapisaæ w innej postaci:
![]() .
.
Wzór ten stanowi ilościowe sformułowanie zasady zgodnej z intuicją i naszymi poprzednimi rozważaniami (porównaj rys. 13); mianowicie skupiająca powierzchnia zmniejsza rozbieżnośæ przechodzącej przez nią wiązki promieni świetlnej (o charakteryzującą tê powierzchniê moc optyczną P).