WYKŁAD 2
1.2 Własności optyczne powierzchni opisanych krzywymi
stożkowymi w oparciu o zasadê Fermata
Omawianie własności optycznych powierzchni stożkowych rozpoczniemy od wprowadzenia tzw równania biegunowego. Oprócz ogólnie znanej postaci kanonicznej równañ opisujących krzywe stożkowe (różnej dla każdej z tych krzywych, tzn dla paraboli, elipsy i hiperboli), istnieje wspólna dla wszystkich tych krzywych postaæ zapisana we współrzêdnych biegunowych.

Rys. 8. Rysunek pomocniczy do wyprowadzenia równania krzywych stożkowych we współrzêdnych biegunowych. F - ognisko krzywej stożkowej, prosta KO - kierownica, MF, f - współrzêdne biegunowe. Punkt M jest punktem "bieżącym".
Wyprowadzenie równania biegunowego dla krzywych stożkowych wykorzystuje nastêpujące wspólne własności geometryczne tych krzywych (rys. 8):
1). Dla dowolnego punktu M leżącego na krzywej zachodzi nastêpująca relacja:
KM× e = MF,
oraz, ponieważ odległośæ kierownicy KO od ogniska F nie może zależec od wyboru punktu M musi zachodziæ dodatkowo nastêpująca relacja:
2). Dla dowolnego punktu M
KM + MF× cosf = OF.
Z warunków 1) i 2) otrzymujemy:
MF/e + MF× cosf = OF,
skąd otrzymujemy wspomnianą wyżej postaæ biegunową:
![]() ,
,
gdzie e oznacza tzw mimośród a p =OF× e jest parametrem ustalającym wzglêdne położenie kierownicy i krzywej. W materiałach pomocniczych pokazujemy krzywe stożkowe obliczone z powyższego równania, po przetransformowaniu ze współrzêdnych biegunowych do współrzêdnych kartezjañskich x, y, dla trzech wybranych wartości e. Jak widaæ z wykresów wartości mimośrodu e < 1 odpowiada elipsa, dla e = 1 otrzymujemy parabolê, a dla e > 1 - hiperbolê. Trochê żmudniejsze ale nietrudne jest udowodnienie, że postaæ biegunowa jest równoważna postaci kanonicznej, znak pewnej wielkości (chyba e2 - 1) decyduje o tym, czy dostaniemy x2 - y2 czy też x2 + y2, czyli hiperbolê czy elipsê (jak e = 1, to jest najprościej i mamy parabolê). Przy okazji dostaje siê różne związki pomiêdzy parametrami e i p, a parametrami a i b, charakterystycznymi dla postaci kanonicznej.
Elipsoida
Własności ogniskujące powierzchni elipsoidalnej przedstawiono na rys. 9. Jak pokazano na rysunku równoległa wiązka światła padająca na taką powierzchniê ulega skupieniu w dalszym z dwóch ognisk elipsoidy (czy elipsy, ze wzglêdu na symetriê osiową układu, możemy bez straty ogólności ograniczyæ siê do rozważenia jednej tylko płaszczyzny, pokazanej na rysunku).

Rys. 9. Równoległa wiązka światła rozchodząca siê w ośrodku o współczynniku załamania n1 pada na układ optyczny w formie elipsoidy obrotowej wykonanej ze szkła o współczynniku załamania n2. Wiązka równoległa transformuje siê w wiązkê kulistą zbieżną do ogniska F. Ze wzglêdu na odwracalnośæ biegu promieni oznacza to także, że rozbieżna wiązka wychodząca z F po wyjściu z układu zostanie przetransformowana w wiązkê równoległą.
Wynika to z nastêpującego rozumowania: czasy przejścia dla różnych promieni równoległej wiązki są jednakowe na każdej płaszczyźnie prostopadłej do wiązki. Możemy wiêc dla dowolnego promienia świetlnego przyjąæ, że czas przejścia pomiêdzy punktami K i K, leżącymi na dwóch kierownicach elipsy byłby stały dla wszystkich promieni KMK, pod warunkiem oczywiście, że tory tych promieni przebiegają w powietrzu. Czas ten wyniósłby
![]() .
.
Z drugiej strony KK = KM + MK a także (patrz rys. 8) MK× e = MF skąd:
![]() .
.
Przyjmując, że e = n1 /n2 (mimośród e dla elipsy musi byæ mniejszy od 1) mamy wobec tego nastêpującą relacjê:
![]() ,
,
której prawa strona przedstawia czas przejścia promienia torem KMF, przy czym odcinek KM światło przebywa w powietrzu (współczynnik załamania n1) a odcinek MF w szkle (współczynnik załamania n2). Ponieważ relacja ta zachodzi dla dowolnego punktu M leżącego na elipsie, udowodniliśmy tym samym, że odpowiednie czasy przejścia dla wszystkich promieni wiązki równoległej, które po załamaniu zbiegają siê w ognisku F, są jednakowe a zatem, że tory KMF dla dowolnego punktu M spełniają zasadê Fermata.
Hiperboloida
Na rysunku 10 przedstawiono własności ogniskujące układu optycznego w formie hiperboloidy obrotowej. Podobnie jak w przypadku układu elipsoidalnego zakładamy, że współczynnik załamania otaczającego ośrodka (powiedzmy, że jest to powietrze) wynosi n1, a szkła, z którego wykonano układ optyczny, n2. Pokażemy, że rozbieżna wiązka światła wychodząca z ogniska hiperboli F transformuje siê, po przejściu przez powierzchniê oddzielającą oba ośrodki, w wiązkê równoległą. W tym celu wystarczy pokazaæ, że czasy przejścia po różnych torach FMK są równe dla dowolnego punktu M leżącego na hiperboli. Przy tym prosta, na której leży punkt K, może byæ w miarê dowolna, byle równoległa do kierownic hiperboli i umieszczona gdzieś w ośrodku n2. Podobnie jak w przypadku elipsy niech t0 oznacza czas przejścia przez światło odcinka KK pomiêdzy jedną z kierownic i tą drugą prostą, ale w szkle, a nie w powietrzu tak jak poprzednio (t0 = KK× n2 / c). Przyjmując tym razem, że e = n2 / n1 (e > 1 dla hiperboli), z relacji KM× e = FM (która obowiązuje w przypadku hiperboli dla obu jej gałêzi niezależnie, którą parê kierownica - ognisko wybierzemy, lewą czy prawą) mamy KM× n2 = FM× n1 i, wobec tego:
![]() ,
,
co oznacza, że czas przejścia z ogniska F do M (w powietrzu) i dalej do punktu K (w szkle) jest stały i nie zależy od wyboru punktu M. cbdo.

Rys. 10. Rozbieżna wiązka kulista pada na powierzchniê hiperboloidalną oddzielającą ośrodek rzadszy (wsp. zał. n1, np. powietrze) od ośrodka gêstszego o współczynniku załamania n2. Wiązka rozbieżna transformuje siê w wiązkê równoległą. Punkt K leży na kierownicy, punkt K zaś na pewnej prostej równoległej do kierownicy.
Paraboloida
Ostatnim przykładem z tej serii bêdzie paraboloida. Oczywiście, ponieważ dla paraboli e = 1, szukamy takiej sytuacji, w której moglibyśmy wykorzystaæ relacjê KM = MF; zatem, o ile nasza taktyka ma byæ taka sama (czyli e powinno byæ zdeterminowane przez współczynniki załamania, tak jak poprzednio) oba odcinki powinny leżeæ w ośrodku o tym samym współczynniku załamania.
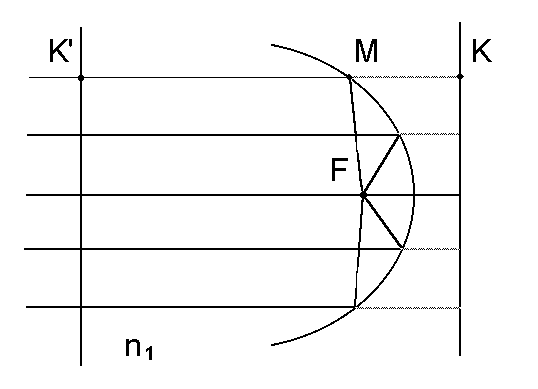
Rys. 11. Wiązka promieni równoległych po odbiciu od powierzchni paraboloidalnej transformuje siê w kulistą wiązkê zbieżną do ogniska F.
Układem optycznym spełniającym taki warunek bêdzie zwierciadło paraboliczne, pokazane na rys. 11. Rzeczywiście, podobnie jak poprzednio, ponieważ dla dowolnego punktu czasy przejścia promienia świetlnego w powietrzu pomiêdzy punktami K i K bêdą jednakowe i równe
![]() ,
,
który to czas, wobec równości MK = MF, bêdzie równy czasowi przejścia w powietrzu po wszystkich torach KMF, dla dowolnego M leżącego na paraboli. Równośæ czasów przejścia, z zasady Fermata oznacza, że równoległa wiązka światła padająca na układ zostanie skupiona w punkcie F lub, innymi słowami, że rzeczywisty obraz nieskoñczenie daleko leżącego punktowego przedmiotu znajdzie siê w ognisku F paraboli (Feynman, t. 1, cz. 2, str. 20).