WYK£AD 14
3.2 Dyfrakcja w ujêciu Fresnela-Kirchhoffa
Ca³ka dyfrakcyjna Fresnela-Kirchhoffa
Sformu³owanie podstaw koncepcyjnych potrzebnych dla rozpatrywania zjawisk dyfrakcji na pojedynczych otworach o ró¿nych kszta³tach zawdziêczamy Huyghensowi, Fresnelowi i Kirchhoffowi. Poniewa¿ podstawy fizyczne (zasada Huyghensa-Fresnela, Babineta, koncepcja fikcyjnych oscylatorów i jej uzasadnienie fizyczne) by³y ju¿ dyskutowane, zatem w tej chwili skupimy siê na przedstawieniu samego formalizmu. Rozwa¿ymy, dla skupienia uwagi, przypadek pojedynczego otworu o dowolnym kszta³cie, pokazanym na rys. 52.
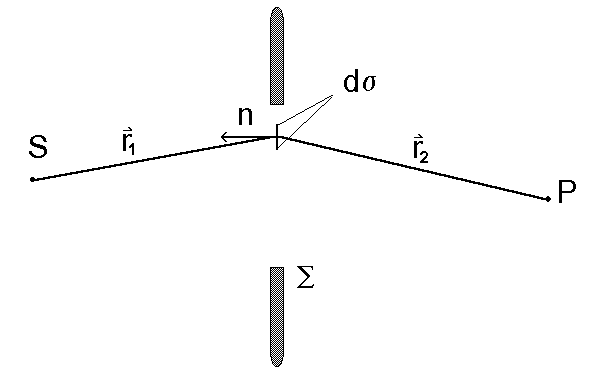
Rys. 52. Fala świetlna dochodząca do punktu P bêdzie superpozycją wtórnych fal emitowanych przez fikcyjne oscylatory roz³o¿one w otworze i wzbudzane przez falê pierwotną emitowaną przez ród³o S.
Przyjmujemy, ¿e ród³o S emituje falê pierwotną w postaci:
![]() .
.
W punkcie P otrzymamy oscylacjê:
![]()
o amplitudzie u0(P), do której wk³ad wniesiony przez element powierzchni otworu ds bêdzie:
 ,
,
gdzie:
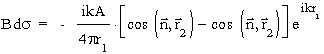 .
.
Ca³a amplituda oscylacji w punkcie P, u0(P) bêdzie dana ca³ką:
 ,
,
po ca³ej powierzchni ekranu (w³aściwie to otworu), która, ³ącznie z poprzednimi wzorami jest czêsto nazywana ca³ką dyfrakcyjną (wzorem dyfrakcyjnym) Fresnela-Kirchhoffa. Nie bêdziemy z tego robiæ ¿adnego u¿ytku, ale chyba warto wiedzieæ, ¿e, jak pokaza³ Kirchhoff, wzór ten mo¿na otrzymaæ poszukując postaci rozwiązania skalarnego równania falowego z odpowiednimi warunkami brzegowymi, narzuconymi przez obecnośæ otworów czy krawêdzi w ekranie. Zauwa¿cie jednak, ¿e poza pewnymi sta³ymi, jak k, -i, 4p , czy czynnik z cosinusami (zapewnia on niewystêpowanie niefizycznej fali wstecznej, która porusza³aby siê w kierunku od otworu do ród³a S) postaæ wzoru jest ca³kowicie zrozumia³a na podstawie fizycznego rozumowania bêdącego podstawą zasady Huyghensa-Fresnela.
Podejście opierające siê na ca³ce Fresnela-Kirchhoffa mo¿na stosowaæ, u¿ywając odpowiednich przybli¿eñ, dla ka¿dej niemal konfiguracji ród³a, otworów i ekranu. Dla przypomnienia, istnieją dwa wa¿ne przypadki. Pierwszy, to gdy zachodzi warunek Fraunhofera (du¿e odleg³ości ród³a i ekranu od otworu, albo tzw pole dalekie); warunek ten przyjêliśmy w naszych rozwa¿aniach nad interferencją na jednakowych otworach, a drugi to tzw dyfrakcja Fresnela wystêpująca dla mniejszych odleg³ości (tzw pole bliskie), kiedy, inaczej ni¿ dla dyfrakcji Fraunhofera, w obrazie wystêpują silnie zmieniające siê z odleg³ością cechy geometryczne (w postaci cienia geometrycznego), jak i wynikające z dyfrakcji (prą¿ki).
Ca³ka Fresnela-Kirchhoffa w przybli¿eniu Fraunhofera
Zgodnie z poprzednimi rozwa¿aniami amplituda fali świetlnej w punkcie P, u0(P) wyrazi siê wzorem Fresnela-Kirchhofa (rys. 53):
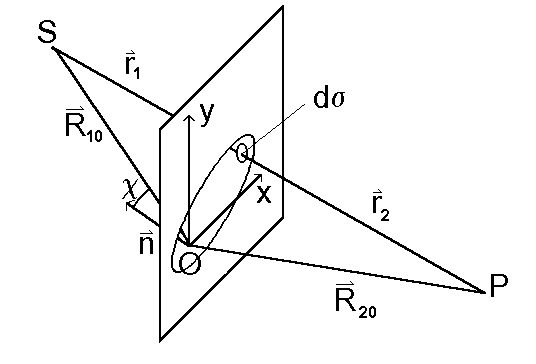
Rys. 53. Dyfrakcja Fraunhofera na otworze. Dla bardzo du¿ych odleg³ości po stronie ród³a S i punktu obserwacji P cos(n,r1) @ cosc , cos(n,r2) @ - cosc . Kąty q 1 i f 1, określające po³o¿enie ród³a, a tak¿e q 2 i f 2, określające po³o¿enie punktu obserwacji P, są określone tak jak poprzednio
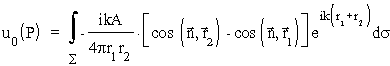 .
.
O ile warunek Fraunhofera jest spe³niony to:
![]() ,
,
a tak¿e
![]() .
.
Wprowadmy specjalnie wybrany punkt P0, taki ¿e q 2 = -q 1 i f 2 = -f 1. Punkt P0 bêdzie le¿a³ na prostej przechodzącej przez S i punkt O, początek uk³adu Oxy w p³aszczynie otworu. Poniewa¿ obraz dyfrakcyjny powinien znajdowaæ siê w otoczeniu punktu P0 zatem spodziewamy siê, ¿e:
![]() .
.
Podobnie jak dla interferencji Fraunhofera na wielu jednakowych otworach mo¿emy przybli¿yæ r1 i r2 przez R10 i R20 dla amplitud, a dla faz skorzystamy z nastêpującego przybli¿enia:
![]() .
.
Wprowadzimy tak¿e funkcjê:

Mamy wówczas:
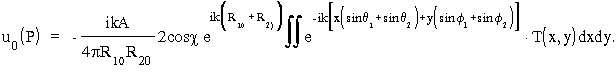
Poniewa¿ dla punktu P0 q 2 = -q 1 i f 2 = -f 1, zatem:

Ostatecznie mamy:
![]()
gdzie:
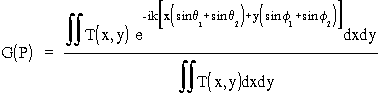
bêdziemy nazywaæ czynnikiem dyfrakcyjnym. Warto zwróciæ uwagê na formalne podobieñstwo pomiêdzy czynnikiem dyfrakcyjnym i interferencyjnym; oczywiste ró¿nice wynikają z faktu, ¿e w jednym przypadku mamy do czynienia z ciąg³ym rozk³adem oscylatorów, którego uwzglêdnienie wymaga ca³kowania, a w drugim z rozk³adem dyskretnym, który mo¿na uwzglêdniæ za pomocą sumowania. Jedna i druga procedura jest jednak oparta na tych samych fizycznych podstawach, co bywa ród³em k³opotów z rozró¿nieniem (dośæ przecie¿ formalnym) pomiêdzy dyfrakcją i interferencją. Praprzyczyna i dyfrakcji i interferencji jest w koñcu ta sama: jest nią falowa natura świat³a.
Oczywiście najbardziej interesuje nas natê¿enie świat³a w punkcie P, które, na podstawie wzoru na amplitudê bêdzie mia³o nastêpującą postaæ:
![]() ,
,
podczas gdy:
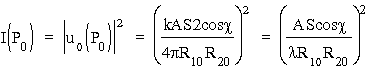 ,
,
gdzie S to powierzchnia otworu, która znalaz³a siê w powy¿szym wzorze w wyniku ca³kowania funkcji T(x,y)), natomiast eksponenta z R10 i R20 zniknê³a wskutek mno¿enia u0 przez u0* . Powy¿szy wzór ma prostą interpretacjê; poniewa¿ natê¿enie świat³a emitowanego przez ród³o S powinno byæ proporcjonalne do A2, a pole powierzchni kuli o promieniu R10 wynosi 4p R102, zatem I0, natê¿enie świat³a padającego na otwór, bêdzie I0 ~ A2/R102. Z kolei W = I0Scosc bêdzie mocą świat³a przechodzącego przez otwór (Scosc bêdzie powierzchnią prostopad³ą do kierunku rozchodzenia siê świat³a z S). Mamy wówczas:
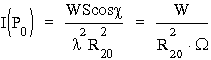 ,
,
gdzie W jest pewnym kątem bry³owym wype³nionym świat³em ugiêtym na otworze. Poniewa¿ iloczyn W × R202 jest proporcjonalny do oświetlonej powierzchni ekranu wobec tego natê¿enie I0(P0) jest, tak jak powinno byæ, mocą świat³a padającego na jednostkê powierzchni ekranu (w punkcie P0). Kąt W powinien byæ wobec tego równy l 2/S× cosc , co ma sens; by³by to po prostu kąt bry³owy określony przez dyfrakcjê, kąt w który skierowana jest du¿a czêśæ świat³a ugiêtego na otworze. Przekonamy siê wkrótce, ¿e rozmiar liniowy pierwszego prą¿ka dyfrakcyjnego na ekranie jest proporcjonalny do d³ugości fali l i odwrotnie proporcjonalny do wymiaru liniowego otworu, podobnie jak dla interferencji. Obecnośæ kwadratu natomiast wynika stąd, ¿e mamy do czynienia z dyfrakcją w dwóch wymiarach.
Dyfrakcja Fraunhofera na otworze prostokątnym
Rozpatrzymy otwór prostokątny o wymiarach axb, pokazany na rys. 54. Zgodnie ze wzorem Fresnela-Kirchhoffa:

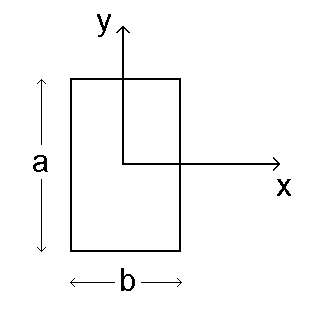
Rys. 54. Otwór prostokątny axb. Początek uk³adu wspó³rzêdnych O wybieramy w środku prostokąta.
Wprowadzimy nastêpujące oznaczenia:
![]() .
.
Podwójna ca³ka w wyra¿eniu na G(P) mo¿e byæ wówczas napisana w nastêpującej postaci:
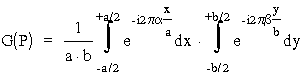 .
.
Ka¿da z pojedynczych ca³ek daje siê ³atwo sca³kowaæ; zrobimy to dla jednej z nich:

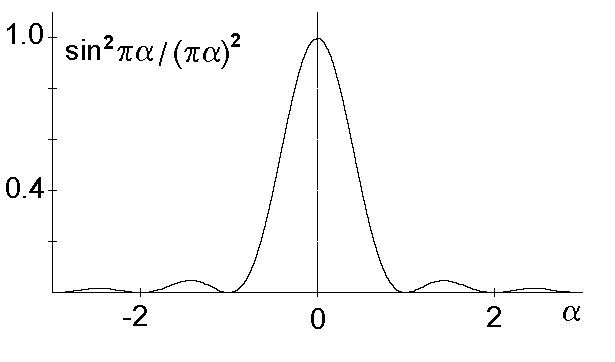
Rys. 55. Jedna z funkcji tworzących czynnik dyfrakcyjny dla prostokątnego otworu.
Podobnie bêdzie z drugą ca³ką, ostatecznie mamy wiêc:
![]() ,
,
a natê¿enie świat³a w punkcie obserwacji P bêdzie:
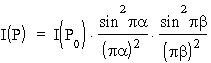 .
.
Pierwsza z dwóch funkcji typu sin2x/x2 wystêpujących w powy¿szym wzorze jest pokazana na rys. 48. Warto zwróciæ uwagê, ¿e parametr a mo¿e byæ traktowany jako odpowiednio unormowana wspó³rzêdna punktu P. Wszystkie zera pokazanej funkcji, z wyjątkiem jednego, odpowiadają zerom funkcji sin, zatem ciemne miejsca na ekranie odpowiadają wartości parametru a (dla drugiej funkcji b ) równej ± 1, ± 2, ± 3, itd. Maksymalną wartośæ otrzymujemy w punkcie a = 0 i to jest wy¿ej wspomniany wyjątek. Natê¿enie w ka¿dym punkcie ekranu jest oczywiście iloczynem dwóch takich funkcji, obraz nie bêdzie siê zatem sk³ada³ z prą¿ków, tylko z plam wystêpujących w punktach przeciêciach jasnych prą¿ków odpowiadających kolejnym maksimom obu omawianych funkcji. Najwiêksze natê¿enia wystąpią zatem w tych plamach dla których przynajmniej jeden z parametrów a i b jest równy zero.
Rozpatrzymy sytuacjê, w której ród³o po³o¿one jest w początku O1 uk³adu wspó³rzêdnych O1X1Y1 (q 1 = f 1 = 0). Dla uproszczenia pomijaæ bêdziemy wskaniki przy q 2 (q 2 = q ) i f 2 (f 2 = f ). Z definicji obu kątów i dla du¿ych odleg³ości R20 = L mamy:
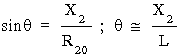 .
.
Z kolei, korzystając z definicji a otrzymamy:
![]() , i podobnie dla b
,
, i podobnie dla b
, ![]() .
.
Tak wiêc otrzymujemy związki pomiêdzy wspó³rzêdnymi punktu P i parametrami a i b w postaci:
![]() ,
,
pokazane dla przypadku parametru a i wspó³rzêdnej X2 na rys. 56.
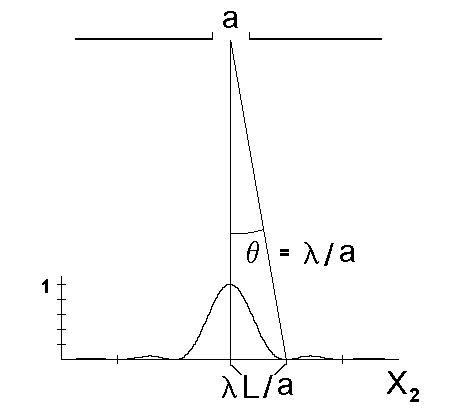
Rys. 56. Związek pomiêdzy wspó³rzêdną X2 i parametrem a . Pierwsze minimum (a = ± 1) odpowiada wartości X2 równej l L/a.
Dyfrakcja Fraunhofera na otworze ko³owym
Drugi przypadek dyfrakcji Fraunhofera, który rozwa¿ymy, to dyfrakcja na otworze ko³owym. Przyjmiemy, ¿e ród³o le¿y w punkcie O1, a punkt P0 wybierzemy w punkcie O. Zatem q 1 = f 1 = 0 i prosta SP, czyli prosta ³ącząca początki uk³adów wspó³rzêdnych O1, O i O2, bêdzie osią symetrii osiowej uk³adu (uk³ad siê nie zmieni po obrocie o dowolny kąt wokó³ osi O1O2). Ze wzglêdu na tê symetriê wystarczy rozpatrzeæ punkty P le¿ące wy³ącznie na osi O2X2, wobec tego mo¿emy przyjąæ, ¿e f 2 = 0 i, dla uproszczenia oznaczeñ, ¿e q 2 = q .
Natê¿enie świat³a w punkcie P, podobnie jak dla otworu prostokątnego, wyniesie:
![]() ,
,
gdzie:
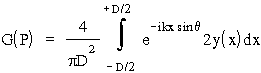 .
.
Wprowadzimy parametr a i uwzglêdnimy zale¿nośæ y (czyli wysokości paska dx) od x (rys. 57):
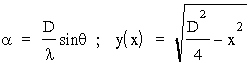 .
.

Rys. 57. Dyfrakcja Fraunhofera na otworze ko³owym. Punkt P0 wybieramy w środku otworu.
Po podstawieniu otrzymamy:
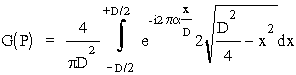 .
.
Wprowadzimy nową zmienną, u = 2x/D, G(P) przyjmie wówczas postaæ:
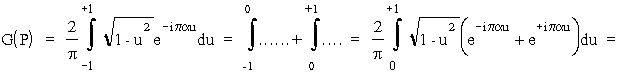
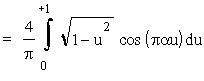 ,
,
gdzie ostatnia ca³ka nie jest ca³ką elementarną; jest to pewna rzeczywista funkcja parametru a nazywaną funkcją Bessela pierwszego rodzaju i pierwszego rzêdu. (Ze wzglêdu na wa¿ną rolê funkcja ta zosta³a stablicowana). Zatem:
 .
.
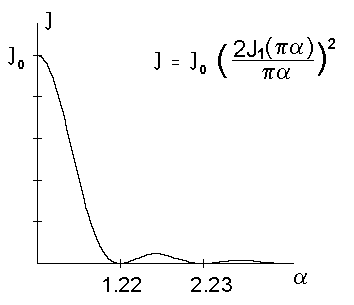
Rys. 58. Rozk³ad natê¿enia na ekranie od otworu ko³owego w funkcji parametru a .
Wykres natê¿enia I w funkcji parametru a przedstawiony jest na rys. 58. Warto zwróciæ uwagê, ¿e pierwsze minimum, inaczej ni¿ dla otworu prostokątnego, przypada dla a = 1.22 (a nie dla a = 1). Odpowiadaæ to bêdzie kątowi:
![]() .
.
Oczywiście to minimum, ze wzglêdu na symetriê osiową, zdefiniuje nie prą¿ek, ale ciemny pierścieñ, otaczający centralny jasny krą¿ek. Centralny krą¿ek nosi nazwê krą¿ka Airyego i, jak mo¿na obliczyæ, zawiera on oko³o 80% ca³kowitej mocy świat³a przechodzącego przez otwór ko³owy. Nastêpne ciemne pierścienie odpowiadają a = 2.23, 3.24 itd.