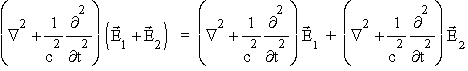 .
. WYK£AD 13
3. OPTYKA FALOWA - INTERFERENCJA, DYFRAKCJA, SPÓJNOŚÆ
3.1 Interferencja i dyfrakcja
Zjawiska interferencji i dyfrakcji związane są z nak³adaniem siê ró¿nych fal (na ile ró¿nych wyjaśnimy dok³adniej potem). Szczególnym przypadkiem bêdzie rozchodzenie siê jednej fali, która przesz³a przez uk³ad szczelin lub ogólniej, otworów. Chodzi o rozk³ad natê¿eñ wynikający z nak³adania siê, w obszarze za otworami, fragmentów tej samej fali, które przesz³y przez ró¿ne otwory.
Podstawą zjawisk interferencji i dyfrakcji jest tzw zasada superpozycji, wynikająca z liniowości równania falowego:
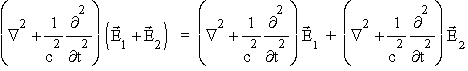 .
.
Jeśli E1 i E2 są rozwiązaniami tego równania to prawa strona jest równa zeru, zatem lewa strona te¿ musi byæ równa zeru, a to oznacza, ¿e E1 + E2 te¿ jest rozwiązaniem. Zasada superpozycji oznacza, ¿e ca³kowite pole elektromagnetyczne jest sumą wszystkich pól wystêpujących w danej objêtości.
Interferencja fal pochodzących z dwóch róde³ punktowych
Zaczniemy od rozpatrzenia szczególnego przypadku interferencji dwóch fal pochodzących z dwóch róde³ punktowych (w przypadku dwóch otworów, albo szczelin, mówimy o doświadczeniu Younga). Niech zatem S1 i S2 bêdą ród³ami fal monochromatycznych o tej samej czêstości i polaryzacji, odleg³ych od siebie o a. Zgodnie z zasadą superpozycji w punkcie P obserwujemy falê świetlną E, która jest sumą fal pochodzących z obu róde³:
 .
.

Rys. 38. S1 i S2 to ród³a fal świetlnych odleg³e od siebie o a (a jest wiêksze od d³ugości fali l ). W odleg³ości L znajduje siê punkt P, w którym obserwujemy falê wypadkową.
Poniewa¿:
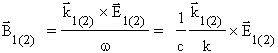
i korzystając znowu z zasady superpozycji mamy:
 ,
,
gdzie wektory falowe k1 i k2 ró¿nią siê kierunkiem (ale nie d³ugością). Wektory Poyntinga (a wiêc strumieñ mocy, czyli energia na jednostkê czasu i powierzchni; czyli natê¿enie) charakteryzujące fale wysy³ane przez ród³a S1 i S2 bêdą równe:
 .
.
Wektor Poyntinga dla wypadkowej fali wyrazi siê poprzez wektory E i B przedstawiające ca³kowite pole pochodzące od obu róde³:
 .
.
Przyjmując, ¿e oba pola E1 i E2 są prostopad³e do obu wektorów falowych k1 i k2 (co mo¿e byæ dok³adnie prawdą dla jednej jpolaryzacji liniowej ale niezupe³nie dla innej, ortogonalnej) otrzymamy dalej:
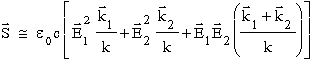 .
.
Niech k1 + k2 = 2k; poniewa¿ dla a < < L mo¿emy przyjąæ, ¿e k1 » k2 zatem k1 » k2 » k i, wobec tego:
![]() ,
,
wynik, który nie jest zbyt zaskakujący; natê¿enie fali wypadkowej wyra¿a siê poprzez wypadkowe pole elektryczne w taki sam sposób jak natê¿enia fal sk³adowych, wysy³anych przez ród³a S1 i S2, przez pola sk³adowe E1 i E2.
Powy¿szy wzór jest bardzo wa¿ny; wyra¿a on bowiem mierzalną wielkośæ, jaką jest wektor Poyntinga, poprzez pole elektryczne, które wystêpuje w teorii (równaniach Maxwella). Warto jednak zwróciæ uwagê, ¿e we wzorze tym wystêpuje kwadrat pola elektrycznego, powinniśmy wiêc byæ ostro¿ni ze stosowaniem zapisu zespolonego. Wydawa³oby siê nawet, ¿e wrêcz nie mo¿na stosowaæ zapisu zespolonego; pamiêtamy przecie¿, ¿e sens fizyczny ma tylko rzeczywista czêśæ wyra¿enia zespolonego tymczasem rzeczywista czêśæ kwadratu wielkości zespolonej zawieraæ bêdzie wk³ad tak¿e od czêści urojonej.
Poniewa¿ czêstości fal elektromagnetycznych są bardzo wysokie (powy¿ej 1014 Hz) nie jesteśmy w stanie z powodów technicznych śledziæ czy mierzyæ chwilowe wartości pola czy natê¿enia (wymaga³oby to rozdzielczości czasowej znacznie poni¿ej femtosekundy). Zresztą nie jest to tylko sprawa techniczna; z tego co wiemy dzisiaj ograniczenie jest bardziej fundamentalne. Po prostu opis klasyczny pola elektromagnetycznego i oddzia³ującej z tym polem materii, korzystający z ciąg³ych w czasie funkcji, nie jest poprawny. Świat nie jest klasyczny; jeśli bêdziemy mierzyæ energiê przekazaną przez pole elektromagnetyczne do jakiegoś detektora w coraz krótszym czasie to jej ilośæ na jednostkê czasu (czyli moc) nie bêdzie sta³a; natkniemy siê w koñcu (po pokonaniu ró¿nych technicznych k³opotów) na granicê kwantową, tzn zauwa¿ymy, ¿e istnieje pewna najmniejsza mo¿liwa porcja energii zwana kwantem, która jest przekazywana do detektora w sposób, na dodatek, dośæ chaotyczny. Ilośæ energii mierzonej w dostatecznie ma³ym przedziale czasowym bêdzie fluktuowaæ, choæ zawsze odpowiadaæ bêdzie ca³kowitej liczbie kwantów (o ile nasza aktualna teoria jest s³uszna; tego nigdy nie mo¿emy byæ pewni na 100%).
Tak wiêc na ogó³ mierzymy nie chwilowe ale średnie w czasie wartości natê¿enia wiązki świat³a. Okazuje siê, ¿e zapis zespolony mo¿e byæ dla obliczania wartości średnich w czasie bardzo przydatny. Obliczmy średnią w czasie wartośæ kwadratu pewnej oscylującej harmonicznie wielkości fizycznej f:
![]() ,
,
po wykorzystaniu definicji średniej wartości z funkcji okresowej, f(t) = f(t+T):
( .
.
Z drugiej strony policzmy wielkośæ ![]() , gdzie
, gdzie ![]() :
:
![]() .
.
A zatem mo¿emy wykorzystaæ zapis zespolony do obliczenia wartości średniej kwadratu oscylującej harmonicznie wielkości fizycznej.
Zastosujemy otrzymany wy¿ej wynik do wektora Poyntinga:
 ,
,
gdzie E01(2) jest zespoloną amplitudą fal emitowanych przez ród³a S1 i S2, odpowiednio. Dla polaryzacji eliptycznej (bierzemy taką w³aśnie polaryzacjê, bo jest to przypadek najbardziej ogólny, ³atwo z niego mo¿na otrzymaæ ka¿dą inną polaryzacjê) E0 = a a + ib b gdzie a i b to wektory jednostkowe dla osi x i y (powiedzmy) le¿ących w p³aszczy¼nie prostopad³ej do kierunku rozchodzenia siê fali k/k (czyli kierunku osi z). Mamy wówczas:
![]() ,
,
a zatem średni w czasie strumieñ mocy świat³a emitowanego ze róde³ S1 i S2 jest proporcjonalny do sumy kwadratów amplitud ka¿dej sk³adowej (tzn x i y) wektorowej pola elektrycznego:
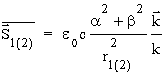 .
.
Oznaczmy średnią wartośæ w czasie wektora Poyntinga literą I (wielkośæ tê bêdziemy nazywaæ, co zresztą ju¿ robiliśmy, po prostu natê¿eniem świat³a):
 .
.
Natê¿enie świat³a w punkcie P bêdzie zatem:
![]() ,
,
gdzie oprócz natê¿eñ świat³a emitowanego przez ród³a S1 i S2 wystêpuje pewien dodatkowy wyraz mieszany (tzw wyraz interferencyjny), którym siê teraz zajmiemy dok³adniej.
O ile czêstości obu fal są dok³adnie równe (co oznacza ca³kowitą spójnośæ) to wyrazy zale¿ne od czasu t znikają i:
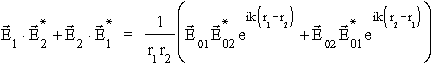 .
.
Przyjmijmy, ¿e polaryzacje obu fal są opisane nastêpującymi amplitudami zespolonymi:
![]() ,
,
mamy wówczas:
![]() .
.
Dla ortogonalnych polaryzacji wyraz interferencyjny znika. Bierze to siê stąd, ¿e dla ortogonalnych polaryzacji g = b , d = -a , co oznacza, ¿e amplitudy obu fal bêdą nastêpujące:
![]() .
.
Z wyra¿eñ tych wynika, ¿e osie g³ówne obu elips są do siebie prostopad³e a kierunki obrotu są przeciwne (dodatni wyraz urojony w pierwszej i ujemny w drugiej amplitudzie). Wiązki świat³a spolaryzowane ortogonalnie nie interferują (poniewa¿ wyraz interferencyjny jest zawsze równy zero), natomiast jeśli polaryzacje obu wiązek są jednakowe to wyraz interferencyjny bêdzie równy:
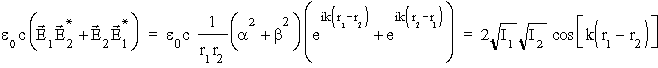 ,
,
zatem mo¿e on byæ dodatni, ujemny jak i równy zero, zale¿nie od argumentu funkcji cosinus. Natê¿enie I świat³a z obu róde³ wyniesie:
![]() ,
,
gdzie d = k(r1 - r2). Maksymalne i minimalne natê¿enia wyniosą odpowiednio:
![]() , interferencja konstruktywna, d
= 2p
m, m = 0, ±
1, ±
2, ±
3, ...
, interferencja konstruktywna, d
= 2p
m, m = 0, ±
1, ±
2, ±
3, ...
![]() , interferencja destrukcyjna, d
= p
(1+ 2m), m = 0, ±
1, ±
2, ±
3, ...
, interferencja destrukcyjna, d
= p
(1+ 2m), m = 0, ±
1, ±
2, ±
3, ...
Jeśli i polaryzacje i natê¿enia obu sk³adowych fal są równe, I1 = I2 = I0 to:
![]() ,
,
przy czym warunki na interferencjê konstruktywną i destrukcyjną są takie same jak poprzednio.
Zauwa¿my, ¿e wykorzystując definicjê d i wektora falowego k (k = 2p /l ), warunek na interferencjê konstruktywną mo¿na przepisaæ w postaci:
![]() ,
,
a l jest d³ugością fali. Warunek ten jest oczywisty; jeśli ró¿nica dróg bêdzie równa wielokrotności d³ugości fali, ró¿nica faz bêdzie wielokrotnością 2p i fale z obu róde³ bêdą w fazie, a wiêc dodadzą siê (dla interferencji destrukcyjnej, ró¿nica dróg musi byæ wielokrotnością l plus l /2; dziêki temu ró¿nica faz wyniesie p , fale bêdą w antyfazie i odejmą siê). Warto tak¿e zwróciæ uwagê, ¿e postaæ tego warunku przypomina geometryczną definicjê hiperboli; hiperbola jest to zbiór (czyli miejsce geometryczne) punktów M, dla ka¿dego z których bezwzglêdna wartośæ ró¿nicy odleg³ości od dwóch danych punktów nazywanych ogniskami hiperboli, jest wielkością sta³ą (jak widaæ, to w³aśnie w ogniskach tej naszej hiperboli powinny znaleæ siê ród³a świat³a S1 i S2).

Rys. 39. Hiperbola, dla której r1 -r2 = ± 8. Odleg³ośæ pomiêdzy ogniskami (punkty S1 i S2) wynosi 10. Dla świat³a o d³ugości fali równej 1, hiperboloida otrzymana przez obrót tej hiperboli wokó³ osi x odpowiada jasnym prą¿kom rzêdu 8.
Na rys. 39 przedstawiamy hiperbolê dla której m = ± 8. Jednostką d³ugości dla obu osi x i y jest d³ugośæ fali świat³a (a wiêc l = 1). Z warunku interferencji (r1 - r2 = l m =2a; zatem a = l m/2) dla m = 8, wynika, ¿e parametr a hiperboli określający odleg³ośæ pomiêdzy jej wierzcho³kami, jest równy 2 (a nie bêdzie ju¿ odleg³ością pomiêdzy ród³ami, jak na rys. 38),. Parametr c, z którym związana jest odleg³ośæ pomiêdzy ogniskami (równa 2c), przyjêliśmy równy 5. Wykreślając hiperbolê z rys. 39 u¿yliśmy jej kanonicznej postaci:
 ,
,
a tak¿e wykorzystaliśmy związek pomiêdzy wspó³czynnikami a, b i c; ![]() .
.
Tak naprawdê, aby u³atwiæ sobie ¿ycie i nie zatykaæ komputera (zastosowany w tym przypadku program matematyczny jest znacznie wolniejszy przy wykreślaniu funkcji zadanych implicite), u¿yliśmy zamiast wzoru w postaci kanonicznej, inny wzór podający bezpośrednio (explicite) zale¿nośæ y od x:
 ,
,
do którego wstawiliśmy policzone wcześniej sta³e parametry. Zmieniając m mo¿na dostaæ ca³ą rodzinê hiperbol, z których ka¿da spe³nia warunek interferencji. Warto zwróciæ uwagê, ¿e w rzeczywistości warunek interferencji konstruktywnej bêdzie spe³niony dla punktów M le¿ących na hiperboloidzie obrotowej, otrzymanej przez obrót hiperboli z rys. 39 wokó³ osi x. Jeśli równolegle do osi x i w pewnej od niej odleg³ości wstawimy p³aski ekran, to przeciêcia p³aszczyzny ekranu z hiperboloidami spe³niającymi warunek konstruktywnej interferencji dadzą jasne prą¿ki. Wydawa³oby siê, ¿e prą¿ki te powinny byæ opisane hiperbolami, to by³oby oczywiście dok³adnie prawdą, gdyby nasza wyjściowa hiperboloida by³a sto¿kiem; przeciêcia sto¿ka p³aszczyznami to są krzywe sto¿kowe, ale czym są przeciêcia p³aszczyzną hiperboloidy obrotowej? Inna rzecz, ¿e na ogó³ odleg³ośæ ekranu od róde³ bêdzie znacznie wiêksza od odleg³ości pomiêdzy nimi; o tyle wiêksza, ¿e nawet dla prą¿ków niskich rzêdów x bêdzie znacznie wiêksze od a. Zatem, po pominiêciu jedynki otrzymujemy przybli¿ony wzór; y = ± bx/a i hiperboloida przechodzi w sto¿ek. £atwo zauwa¿yæ, ¿e pomiêdzy prą¿kami jasnymi, dla których warunek konstruktywnej interferencji jest spe³niony, wystąpią prą¿ki ciemne, dla których spe³niony bêdzie warunek interferencji destrukcyjnej.
W p³aszczy¼nie xy wspó³rzêdna x bêdzie opisywaæ po³o¿enie prą¿ka na ekranie ,a wspó³rzêdna y oznaczaæ bêdzie odleg³ośæ ekranu od róde³ świat³a, tak jak pokazano na rys. 40.

Rys. 40. Geometria uk³adu do obserwacji prą¿ków interferencyjnych w doświadczeniu Younga. S1 i S2 to ród³a (szczeliny) świat³a w odleg³ości d od siebie. Ekran umieszczony jest w odleg³ości L od róde³, punkt obserwacji na ekranie, oznaczony literą P, le¿y w odleg³ości x od punktu odniesienia P0.
Poniewa¿: ![]() , z warunku interferencji mamy a = l
m/2, y = L, a odleg³ośæ róde³ d w wyra¿ona poprzez parametr hiperboli d = 2c, zatem:
, z warunku interferencji mamy a = l
m/2, y = L, a odleg³ośæ róde³ d w wyra¿ona poprzez parametr hiperboli d = 2c, zatem:
 .
.

Rys. 41. Dla du¿ych odleg³ości L mo¿na przyjąæ, ¿e promienie r1 i r2 są praktycznie równoleg³e i ró¿nicê dróg r1 - r2 = D mo¿na wyraziæ przez kąt a , D /d @ a .
Otrzymaliśmy ogólnie znany wzór podający odleg³ośæ na ekranie prą¿ka rzêdu m od prą¿ka zerowego (w punkcie P0). Wzór ten ³atwo zrozumieæ; jak pokazuje rys. 41, dla dostatecznie du¿ych L mo¿na przyjąæ, ¿e r1 i r2 są praktycznie równoleg³e i ró¿nica dróg dla obu promieni jest równa D . Mamy wówczas jednocześnie (z rys. 40 i 41):
![]()
oraz:
![]() .
.
Dla ma³ych a sina @ tga @ a zatem:
![]() ,
,
skąd ju¿ bezpośrednio wynika otrzymany przez nas wcześniej uproszczony wzór, xm = m× L× l /d. Dla prą¿ków ciemnych mo¿na ³atwo pokazaæ, ¿e xm+1/2 = (m+1/2)× L× l /d. Zgodnie z powy¿szym przybli¿eniem, mo¿emy tak¿e przyjąæ, ¿e:
![]() ,
,
a poniewa¿ ![]()
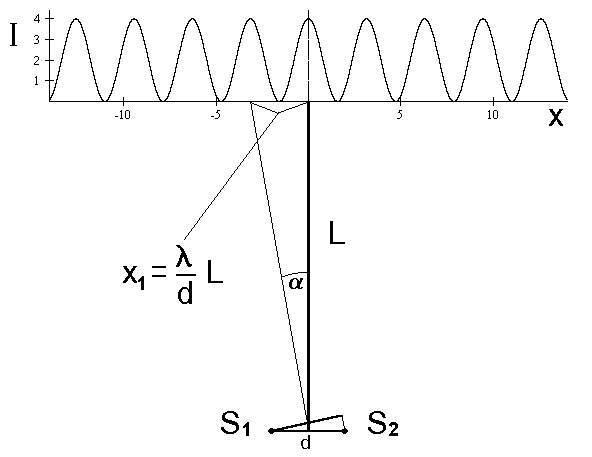
Rys. 42. Rozk³ad natê¿eñ na ekranie dla dwóch róde³ (szczelin). Odleg³ośæ pomiêdzy prą¿kami jasnymi wynosi x = L× l /d.
Na rys. 42 pokazujemy wykres natê¿enia na ekranie dla dwóch róde³ (szczelin). Jednostka d³ugości wspó³rzêdnej x na ekranie jest tak dobrana, by wielkośæ 2Ll /d by³a równa jeden. Inne pokazane d³ugości, a mianowicie L i d, nie są wyra¿one w tej samej jednostce, a wiêc proporcje na rys. 42 nie są zachowane. Natê¿enie świat³a z pojedynczego ród³a przyjêliśmy równe 1; maksymalne natê¿enie w prą¿ku jasnym wynosi wówczas 4, zgodnie z poprzednio wyprowadzonymi wzorami. Średnia wartośæ natê¿enia na ekranie jednak wyniesie 2, jest wiêc po prostu sumą natê¿eñ z obu róde³. Zasada zachowania energii jest zatem spe³niona, interferencja mo¿e co prawda wp³ynąæ na przestrzenny rozk³ad natê¿eñ ale zachowuje przy tym ca³kowitą wartośæ, która musi byæ i jest równa sumie natê¿eñ emitowanych przez wszystkie interferujące ze sobą ród³a.
Dyfrakcja i interferencja na otworach
Rozpatrzymy teraz zjawiska związane z przechodzeniem świat³a emitowanego przez jedno ród³o S przez nieprzeroczysty ekran z otworami (rys. 43), który zosta³ umieszczony w pewnej odleg³ości L1 od ród³a S (rys. 44). Interesuje nas taka sytuacja, gdy wymiary otworów i odleg³ości pomiêdzy nimi są porównywalne z d³ugością fali świat³a ze ród³a S. Przyjmujemy tak¿e, ¿e otworów jest N i ¿e są one jednakowe. Po przeciwnej stronie ekranu z otworami w odleg³ości L2 znajduje siê drugi ekran, s³u¿ący do obserwacji wytworzonych obrazów; na ekranie tym le¿y punkt obserwacji P.

Rys. 43. Uk³ad otworów wykonanych w nieprzeroczystym ekranie. Okrąg C obejmuje wszystkie otwory.
Okazuje siê, ¿e w opisanych wy¿ej warunkach stosunkowo ³atwo zaobserwowaæ mo¿na obrazy, których nie da siê wyt³umaczyæ przy pomocy optyki geometrycznej i których wyt³umaczenie wymaga uwzglêdnienia falowej natury świat³a. Niektóre cechy tych obrazów związane są z kszta³tem i wymiarami pojedynczego otworu (wystêpują one nawet wtedy, gdy wszystkie otwory, z wyjątkiem jednego, są zas³oniête); inne zaś zale¿ą od liczby i wzajemnej orientacji otworów ods³oniêtych. W związku z tym rozró¿niamy zjawisko dyfrakcji, czyli ugiêcia fali świetlnej na pojedynczym otworze i zjawisko interferencji, związane ze wzajemnym oddzia³ywaniem nak³adających siê fal świetlnych przechodzących przez ró¿ne otwory.
Zasada Huyghensa-Fresnela i zasada Babineta
Wyobramy sobie najpierw, ¿e pomiêdzy ród³em S i punktem obserwacyjnym P nie ma ¿adnego ekranu, wówczas pole w punkcie P bêdzie ca³kowicie określone przez pole fali świetlnej ES emitowanej przez ród³o S:
![]() .
.
Świadomie pomijamy strza³ki; przechodzimy bowiem do prostszego opisu skalarnego świat³a, w którym zaniedbuje siê polaryzacjê (jest to podejście, którego u¿ywali Huyghens, Fresnel i Kirchoff, autorzy sformu³owania teorii inteferencji i dyfrakcji, które w³aśnie wprowadzamy. W nastêpnym kroku wyobramy sobie, ¿e pomiêdzy ród³o S i punkt P wprowadziliśmy ekran, ale ¿e wszystkie jego otwory są zas³oniête. Mamy wówczas:
![]() ,
,
gdzie E2(P) jest ca³kowitym polem fali świetlnej w punkcie P, a Eekran i Ezatyczki oznaczają pola wyindukowane dziêki obecności odpowiednio, ekranu z otworami i zatyczek zamykających te otwory. Oczywiście, poniewa¿ ekran jest nieprzeroczysty i otwory są zas³oniête, pole to musi byæ równe zero. Istnienie pól Eekran i Ezatyczki wynika wprost z zasady superpozycji; jeśli wskutek wprowadzenia do uk³adu materii, jakieś, obecne przedtem pola znikają, to musi to byæ konsekwencją wytworzenia przez tê materiê odpowiednich kompensujących pól. Fizyczne pochodzenie tych pól nie jest wcale takie tajemnicze; materia sk³ada siê przecie z ³adunków elektrycznych, które pod wp³ywem zewnêtrznych pól elektrycznych bêdą wykonywaæ drgania wytwarzając dziêki temu te dodatkowe pola o tej samej czêstości.
Przy ods³oniêtych otworach (oczywiście jest to sytuacja, która nas najbardziej interesuje):
![]() ,
,
a wiêc, z dwóch ostatnich równañ mamy:
![]() .
.
Jest to bardzo interesujący i mo¿e trochê zaskakujący wynik; pole pochodzące od fali świetlnej za ekranem z otworami jest, z dok³adnością do znaku, równe polu pochodzącemu od zatyczek zas³aniających otwory. Wynik ten stanowi podstawê tzw zasady Huyghensa-Fresnela która opiera siê na idei fikcyjnych oscylatorów roz³o¿onych na powierzchni wszystkich otworów. Dok³adniejsze sformu³owanie ilościowe tej zasady od³o¿ymy na póniej. Inny ciekawy wniosek, wynikający z powy¿szych rozwa¿añ, stanowi podstawê zasady Babineta; która mówi, ¿e poniewa¿ ES + Eekran + Ezatyczki = 0, zatem pola od otworów i komplementarnych do nich zatyczek są z dok³adnością do znaku i pola ES (czêsto pomijalnego) sobie równe; spodziewamy siê zatem, ¿e obrazy dyfrakcyjne od szczeliny i prêta o tej samej szerokości bêdą podobne.
Przybli¿
enie FraunhoferaPrzejdziemy teraz do dok³adniejszych ilościowych rozwaañ. Zaczniemy od wprowadzenia pewnych przybli¿eñ. Okrąg C (pokazany na rys. 43) wyznacza podstawê dwóch sto¿ków, których wierzcho³ki znajdują siê w punktach S i P (rys. 44). Dyfrakcjê i interferencjê w takim uk³adzie nazwiemy fraunhoferowską, gdy odchylenia D sferycznych powierzchni falowych S
1 i S
2 (rys. 44) zawartych w tych sto¿kach, od p³aszczyzn bêdą znacznie mniejsze od d³ugości fali l
świat³a emitowanego przez ¿ród³o S; powiedzmy, ¿e są one rzêdu l
/10, czyli ![]() . Warunek ten oznacza, ¿e z dobrym przybli¿eniem mo¿emy traktowaæ fale wychodzące z S i dochodzące do P jako fale p³askie a nie kuliste.
. Warunek ten oznacza, ¿e z dobrym przybli¿eniem mo¿emy traktowaæ fale wychodzące z S i dochodzące do P jako fale p³askie a nie kuliste.
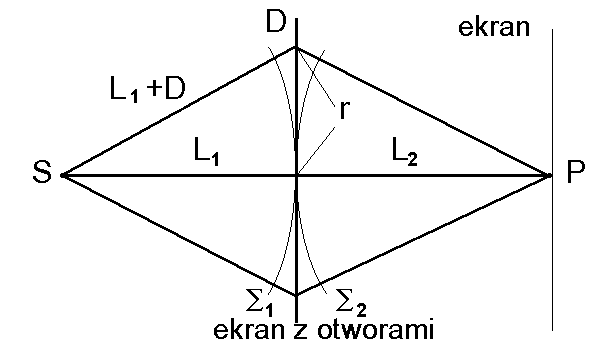
Rys. 44. Uk³ad do obserwacji interferencji i dyfrakcji Fraunhofera na N jednakowych otworach w nieprzeroczystym ekranie w odleg³ości L1 od ród³a świat³a S. Nastêpny ekran i umieszczony na nim punkt obserwacyjny P, znajdują siê w odleg³ości L2 od ekranu z otworami, po przeciwnej jego stronie. r jest promieniem okrêgu C obejmującego otwory.
Poniewa¿:
![]() , a wiêc
, a wiêc  ,
,
gdzie r jest promieniem okrêgu C, na którym oparte są oba sto¿ki. Zatem:
 .
.
Przyjmując r » 1 cm i l » 0.5 m (czyli 500 nm) otrzymujemy L » 103 m (czyli 1 km), ca³kiem sporo jak na typowe warunki laboratoryjne. Jest oczywiste, ¿e nie jest ³atwo spe³niæ takie warunki w laboratorium, póniej dowiemy siê, jak mo¿na tego dokonaæ stosując odpowiednie uk³ady optyczne (soczewki).
W warunkach dyfrakcji i interferencji fraunhoferowskiej (tzn gdy odleg³ości L1 i L2 spe³niają powy¿szy warunek) geometryczny obraz pojedynczego otworu powinien mieæ rozmiary liniowe rzêdu:
 ,
,
gdzie a jest szerokością otworu. Tymczasem obraz dyfrakcyjny pojedynczego otworu (uzasadnienie trochê póniej) bêdzie mia³ rozmiary rzêdu:
![]() .
.
Warunek, by obraz dyfrakcyjny by³ znacznie wiêkszy rozmiarami od obrazu geometrycznego sprowadza siê zatem do:
![]() , a wiêc
, a wiêc 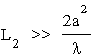 .
.
Porównanie otrzymanego wy¿ej warunku z warunkiem fraunhoferowskim pokazuje, ¿e jest on automatycznie spe³niony; dla dyfrakcji i interferencji fraunhoferowskiej mamy bowiem L ³ 5r2/l . Wynika to stąd, ¿e r, bêdzie wiêksze od a (tymbardziej r2 > a2), gdy¿ r jest promieniem okrêgu obejmującego wszystkie otwory, a tymczasem a jest wymiarem pojedynczego otworu. W warunkach fraunhoferowskich, obrazy dyfrakcyjne pojedynczych otworów są zatem nie tylko jednakowe, ale z dobrą dok³adnością nak³adają siê na siebie. Fakt ten wykorzystamy przy matematycznym opisie interferencji świat³a ugiêtego na wielu otworach.
Interferencja i dyfrakcja Fraunhofera na N jednakowych otworach
Rozwa¿ania nad interferencją i dykfrakcją Fraunhofera na N jednakowych otworach zaczniemy od wprowadzenia odpowiednich uk³adów wspó³rzêdnych, pokazanych na rys. 45.
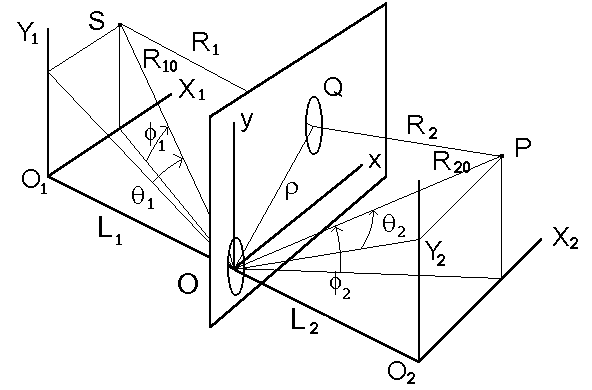
Rys. 45. Uk³ady wspó³rzêdnych do opisu dyfrakcji i interferencji Fraunhofera na N jednakowych otworach. Podczas gdy odleg³ości R (punktów S i P od otworów) są du¿e (rzêdu 103 m), odleg³ości r (pomiêdzy otworami) są ma³e (rzêdu 10- 4 m lub mniejsze).
Na rys. 45 po³o¿enie ród³a S opisane jest wspó³rzêdnymi X1, Y1, w uk³adzie O1X1Y1Z, otworów w ekranie wspó³rzêdnymi x, y w uk³adzie O, x, y, z i, w koñcu punktu obserwacji P wspó³rzêdnymi X2, Y2 w uk³adzie O2X2Y2Z. Oś Z jest wspólna dla wszystkich trzech uk³adów. Punkt O wybieramy tak, by le¿a³ on w jednym z otworów, w miarê mo¿liwości blisko środka okrêgu C. Po³o¿eniom równowa¿nych punktów le¿ących w innych otworach przypisujemy wspó³rzêdne (xi, yi), które wyznaczają po prostu po³o¿enia innych otworów. Odleg³ości O1O i OO2 bêdziemy oznaczaæ tak jak poprzednio L1 i L2.
Poniewa¿ obrazy (czyli natê¿enia) fal ugiêtych na pojedynczych otworach (innymi s³owy wyemitowanych przez fikcyjne oscylatory, roz³o¿one na powierzchni otworów) są jednakowe (i nak³adają siê) zatem fale te powinny mieæ takie same amplitudy, a ró¿niæ siê bêdą tylko fazą. Ró¿nica faz bêdzie przy tym wynika³a nie tylko z ró¿nicy odleg³ości tych otworów od punktu P (tak jak dla rozwa¿anych poprzednio dwóch róde³) ale tak¿e z ró¿nicy odleg³ości pomiêdzy ród³em S i otworami (spowoduje to przesuniêcie w czasie wzbudzenia fikcyjnych oscylatorów rozmieszczonych w otworach). Przyjmijmy zatem, ¿e fala świetlna w punkcie P, pochodząca od otworu QO, któremu przyporządkowany jest początek O uk³adu wspó³rzêdnych na p³aszczynie ekranu, bêdzie opisana wyra¿eniem:
 ,
,
gdzie Eprzestrz(QO,S) jest amplitudą pola w otworze QO pochodzącego od fali pierwotnej wyemitowanej przez ród³o S. W podejściu tym przyjmujemy, ¿e wszystkie oscylatory przypisane jednemu otworowi są wzbudzane w taki sam sposób, pomijamy zatem wzglêdnie ma³e ró¿nice faz związane z przestrzennym rozk³adem tych oscylatorów na powierzchni samego otworu.
Oczywiście uśrednione w czasie natê¿enie świat³a w punkcie P (od tej jednej fali) bêdzie proporcjonalne do E(P,QO)× E* (P,QO), tak jak to udowodniliśmy dla wektorowych fal monochromatycznych.
Fala świetlna w punkcie P, pochodząca od otworu Q, po³o¿enie którego opisuje punkt (x,y) (rys. 38) bêdzie:
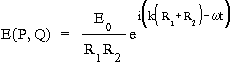 .
.
Pomijając ma³o wa¿ne (w przybli¿eniu Fraunhofera) ró¿nice w amplitudach, a zachowując wa¿niejsze ró¿nice w fazach (nie mo¿emy przecie¿ pominąæ wszystkich ró¿nic!) otrzymamy:
 ,
,
gdzie D 1 = R1 - R10 i D 2 = R2 - R20, to geometryczne ró¿nice dróg optycznych dla promieni (fal) przechodzących drogi SQP i SQOP. Wprowadzimy tak¿e inną wielkośæ, ró¿nicê dróg optycznych (chyba ju¿ kiedys u¿ywaliśmy tego pojêcia):
![]() ,
,
zatem:
![]() .
.
Zbadajmy dok³adniej wielkości D 1 i D 2. Z odpowiednich trójkątów mamy:
![]() ,
,
skąd, po odpowiednich przekszta³ceniach:
 ,
,
gdzie r 2 = x2 + y2 jest odleg³ością otworu Q od otworu "odniesienia" QO. Poniewa¿ r < < R1, R10 mo¿emy pominąæ pierwszy wyraz i, dodatkowo, jeśli uwzglêdnimy, ¿e R1 @ R10 otrzymamy:
 .
.
Ostatecznie oba cz³ony tworzące ca³kowitą ró¿nicê dróg geometrycznych bêdą równe:
Aby znaleæ pole pochodzące od wszystkich otworów trzeba wykonaæ sumowanie:
 .
.
Poniewa¿ uśrednione w czasie natê¿enie I bêdzie proporcjonalne do E(P)× E* (P) otrzymamy:
![]() ,
,
gdzie I1 (P) bêdzie natê¿eniem w punkcie P pochodzącym od pojedynczego otworu (a zatem zawierającym czynnik dyfrakcyjny powstający wskutek superpozycji fal emitowanych przez fikcyjne oscylatory modelujące pojedynczy otwór), natomiast wielkośæ:
 ,
,
zawierającą wk³ady od wszystkich otworów nazywaæ bêdziemy czynnikiem interferencyjnym. Tak wiêc otrzymaliśmy wynik, który, zgodnie z obserwacjami eksperymentalnymi mówi, ¿e rozk³ad natê¿enia od wielu otworów bêdzie odpowiada³ rozk³adowi natê¿enia od jednego otworu zmodyfikowanemu przez pewien czynnik zale¿ny od liczby i wzajemnej orientacji wszystkich otworów.
Dwa otwory - doświadczenie Younga
Dla dwóch otworów rozmieszczonych na osi x w odleg³ości d jeden od drugiego mamy:
N = 2, x1 = y1 = 0, x2 = d, y2 = 0,
wobec tego:
![]() .
.
Czynnik F bêdzie sk³ada³ siê z dwóch wyrazów odpowiadających obu otworom:
![]() ,
,
a natê¿enie świat³a na ekranie obserwacyjnym bêdzie proporcjonalne do czynnika interferencyjnego w postaci:
![]() ,
,
a tak¿e do pewnego czynnika dyfrakcyjnego zale¿nego od kszta³tu otworów. Wynik ten jest identyczny z otrzymanym poprzednio wynikiem dla interferencji fal emitowanych przez dwa ród³a; ró¿nica wynika wy³ącznie z innej definicji d (obie d ró¿nią siê czynnikiem 2p ). Obliczenie czynnika F dla przypadku dwóch otworów mo¿na tak¿e wykonaæ geometrycznie (rys. 46).
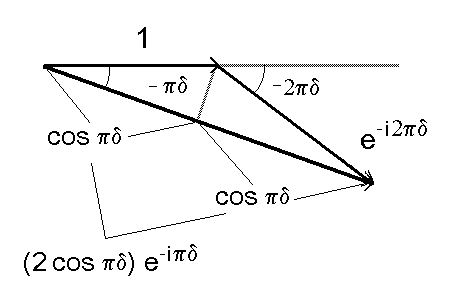
Rys. 46. Obliczanie czynnika F dla dwóch otworów. Dodajemy dwie liczby zespolone, jedynkê i liczbê e-i2p d , przedstawione jako wektory na p³aszczynie zespolonej. Z w³asności trójkąta równoramiennego wnioskujemy, ¿e suma tych dwóch liczb jest liczbą zespoloną o module 2cosp d i kącie -p d .
Ze wzglêdu na brak zale¿ności od f , dla wszystkich punktów S i P, le¿ących na sto¿kach obrotowych, dla których kąty pomiêdzy tworzącymi i osiami obrotu wynoszą odpowiednio q 1 i q 2, bêdziemy mieli sta³e wartości D 1 i D 2. Oznacza to tak¿e sta³e d , które określi wartośæ natê¿enia świat³a. (Nie otrzymaliśmy teraz hiperboloid tylko sto¿ki, ze wzglêdu na zastosowane przybli¿enia - przedtem byliśmy dok³adniejsi, stąd ró¿nica). Oczywiście przeciêcie tych sto¿ków p³aszczyzną (ekranem) wyznaczy miejsca geometryczne punktów o sta³ym natê¿eniu; jeśli natê¿enie to bêdzie maksymalne bêdą to prą¿ki jasne, a jeśli minimalne, to ciemne. W tym przybli¿eniu prą¿ki te bêdą opisane krzywymi sto¿kowymi; w przypadku gdy p³aszczyzna ekranu bêdzie równoleg³a do osi Ox bêdą to hiperbole.
Rozpatrzmy przypadek, gdy ród³o S znajduje siê na wprost obu otworów. Mamy wtedy:
![]() .
.
Z postaci czynnika FF* (= 4cos2 p d ) wynika, ¿e prą¿ki jasne odpowiadają d = n; gdzie n = 0, ± 1, ± 2, ± 3,.... itd; n nazywaæ bêdziemy rzêdem prą¿ka.
Podstawiając warunek na prą¿ek jasny d = n, stosując przybli¿enie ma³ych kątów otrzymamy:
![]() ,
,
wzory na kąty ugiêcia dla prą¿ków rzêdu n i ich po³o¿enia na ekranie, które otrzymaliśmy ju¿ poprzednio dla dwóch spójnych róde³ świat³a.
N jednakowych równoodleg³ych otworów le¿ących na prostej
Dla N jednakowych i równoodleg³ych otworów le¿ących na prostej Ox bêdziemy mieli:
y1 = y2 = y3 = .... = yN = 0;
oraz
x1 = 0, x2 = d, x3 = 2d, x4 = 3d, ...., xN = (N-1)d.
Zatem czynnik interferencyjny F bêdzie równy:
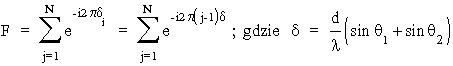 jest d³ugością optyczną.
jest d³ugością optyczną.
Po rozpisaniu mamy:
![]()
 , gdzie
, gdzie ![]() .
.
Po podstawieniu otrzymamy nastêpujące wyra¿enie na F:
 .
.
Natê¿enie fali świetlnej w punkcie P bêdzie zatem proporcjonalne do:
 ,
,
gdzie, dla przypomnienia, ![]() , a kąty q
, a kąty q
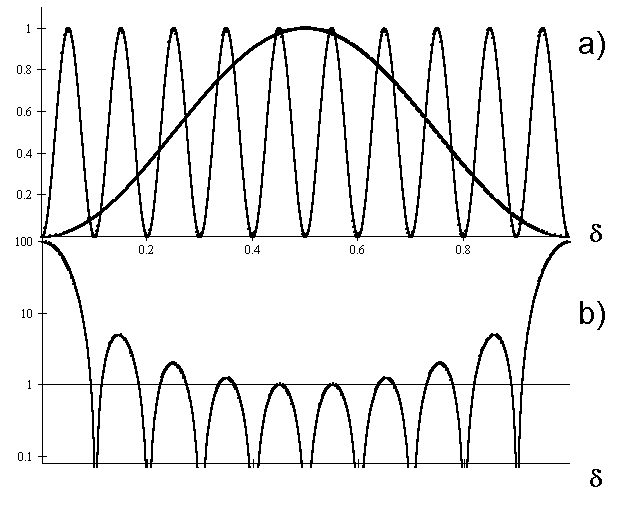
Rys. 47. W czêści a) przedstawione są dwie funkcje tworzące licznik i mianownik wyra¿enia na ç Fç 2 dla uk³adu równoodleg³ych 10 otworów umieszczonych na osi x. W czêści b) przedstawiono ich iloraz. Warto zwróciæ uwagê, ¿e skala osi y jest liniowa w a) i logarytmiczna w b) (trzy rzêdy wielkości). Zakres zmienności d od 0 do 1 obejmuje pe³ny okres periodycznej funkcji opisującej ç Fç 2.
Na rys. 47 a) przedstawiamy dwie funkcje tworzące czynnik interferencyjny dla uk³adu 10 równoodleg³ych i jednakowych otworów rozmieszczonych na osi Ox. Poniewa¿ funkcja sin2p d jest funkcją periodyczną z okresem zmiennej niezale¿nej d równym jeden, a okres argumentu funkcji sin2Np d jest równy 1/N (czyli jest podwielokrotnością okresu funkcji sin2p d ), zatem ca³a funkcja ç Fç 2 = sin2Np d /sin2p d , pokazana na rys. 40 b), bêdzie tak¿e okresowa z okresem zmiennej d równym jeden. Dla d ca³kowitych (d = m; m = 0, ± 1, ± 2, ± 3,... itd,) wyra¿enie
sin2Np d /sin2p d
jest nieoznaczone (typu 0/0); przybliając funkcje z licznika i mianownika poprzez ich argumenty (dla d @ 0) otrzymamy:
 .
.
Dla innych d ca³kowitych, ze wzglêdu na okresowośæ funkcji jej wartości muszą byæ takie same i równe N2. Bêdą to wartości maksymalne a odpowiadające im prą¿ki jasne bêdziemy nazywali prą¿kami g³ównymi. Inne lokalne maksima funkcjiç Fç 2 odpowiadaæ bêdą maksimom funkcji sin2Np d (a nie jej zerom, jak w przypadku maksimów g³ównych), a ich wartości bêdą znacznie mniejsze, rzêdu 1. Bêdą one odpowiada³y tak zwanym jasnym prą¿kom bocznym albo wtórnym, a bêdzie ich, pomiêdzy prą¿kami g³ównymi, N-2. Prą¿ki jasne rozdzielone są prą¿kami ciemnymi, których bêdzie, pomiêdzy prą¿kami g³ównymi, N-1. Szerokości prą¿ków g³ównych są odwrotnie proporcjonalne do N; nieco dok³adniej, dwa zera ograniczające prą¿ek g³ówny bêdą od siebie odleg³e o 2/N (patrz rys. 40). Fakt ten t³umaczy proporcjonalnośæ natê¿enia w maksimum g³ównym do kwadratu liczby otworów; spodziewamy siê proporcjonalności ca³kowitego natê¿enia do N, ca³kowitej liczby otworów (zasada zachowania energii) i tak rzeczywiście jest; poniewa¿ jednak ta sama ilośæ świat³a (proporcjonalna do N) przypada na prą¿ek, którego szerokośæ maleje z N, natê¿enie w maksimum musi rosnąæ z kwadratem N tak by iloczyn maksimum i szerokości pozosta³ sta³y. Ze wzrostem liczby otworów przybywa maksimów wtórnych i prą¿ków ciemnych, a prą¿ki g³ówne robią siê coraz wê¿sze i jaśniejsze. Zbiór punktów o sta³ej wartości d , której odpowiadaæ bêdzie sta³e natê¿enie świat³a, bêdzie nale¿a³ do powierzchni q 2 = const; powierzchnia ta bêdzie sto¿kiem o wierzcho³ku w punkcie O (rys. 45) o osi le¿ącej na osi Ox, wzd³u¿ której le¿ą otwory.
Siatki dyfrakcyjne
W³asności uk³adu wielu równoleg³ych i równoodleg³ych szczelin zosta³y wykorzystane w tzw siatkach dyfrakcyjnych, które umo¿liwiają jeden z najdok³adniejszych pomiarów (d³ugości fali świat³a) rutynowo wykonywanych przez fizyków pracujących w wielu ró¿nych dzia³ach fizyki. Pierwsze siatki dyfrakcyjne zosta³y wykonane przez Fraunhofera ju¿ w 1820 roku.
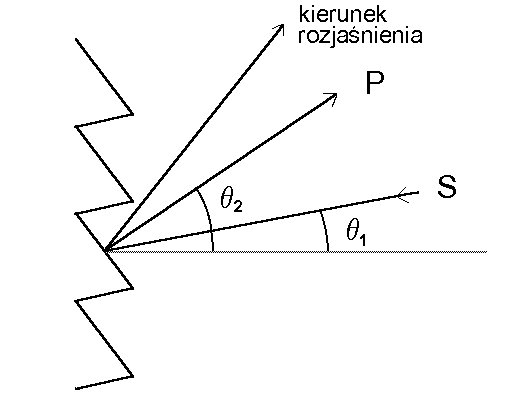
Rys. 48. Odbiciowa siatka dyfrakcyjna (fragment). Dla określonego kąta padania q 1, kąt q 2 bêdzie miarą d³ugości fali świat³a ugiêtego na siatce w kierunku punktu P (patrz tekst). Kierunek "rozjaśnienia" wyznaczony jest przez warunek równości kątów padania i odbicia wzgledem normalnej do powierzchni "zêbów" siatki, pe³niących rolê szczelin (rys). "Szerokośæ kątowa" rozjaśnienia, czyli zakres siatki, zale¿y od szerokości pojedynczego "zêba", która określa wielkośæ dyfrakcji, a zatem tak¿e kątową szerokośæ obrazu dyfrakcyjno - interferencyjnego.
Podstawowy rodzaj siatki dyfrakcyjnej, to tzw siatka odbiciowa "rozjaśniona" pokazana na rys. 48. Poniewa¿ maksima g³ówne siatki dyfrakcyjnej, która jest przecie¿ uk³adem N równoodleg³ych i równoleg³ych szczelin spe³niaæ muszą warunek:
![]()
gdzie m bêdziemy nazywaæ rzêdem siatki, zatem dla ustalonego kąta padania q 1 (powiedzmy, ¿e q 1 = 0), dla ka¿dego rzêdu siatki m bêdziemy mieli wzajemnie jednoznaczne przyporządkowanie pomiêdzy kątem q 2 i d³ugością fali l . A wiêc pomiar d³ugości fali mo¿na sprowadziæ do pomiaru kąta, albo po³o¿enia odpowiedniego prą¿ka, który to pomiar mo¿e byæ bardzo dok³adny. W praktyce robi to siê najczêściej nieco inaczej; przy ustalonych kierunkach do punktów P i S (których rolê grają szczeliny wyjściowa i wejściowa spektrometru), obracamy ca³ą siatką i mierzymy jej kąt obrotu. Mamy wówczas:
![]() ,
,
gdzie a jest kątem obrotu siatki, zaś a 0 jest pewnym sta³ym kątem, którego wielkośæ wynika z technicznych rozwiązañ dla danego typu spektrometru. Przyrządy takie czêsto nazywa siê monochromatorami; inna nazwa, spektrograf, jest zarezerwowana dla przyrządu w którym nie ma szczeliny wyjściowej. Zamiast szczeliny stosowa³o siê dawniej p³yty fotograficzne, a dzisiaj optyczne analizatory wielokana³owe. Bardzo wa¿ną sprawą jest rozdzielczośæ spektralna takich przyrządów, tzn zdolnośæ rozró¿nienia dwóch bliskich d³ugości fali. Pytanie jest nastêpujące: jak ma³o mogą siê ró¿niæ dwie d³ugości fali by odpowiadające im, lekko przesuniête prą¿ki g³ówne, nie zlewa³y siê i ¿eby mo¿na by³o ciągle jeszcze je rozró¿niæ?

Rys. 49. Kryterium Rayleigha. Dwa prą¿ki g³ówne, odpowiadające ró¿nym d³ugościom fali l mo¿na rozró¿niæ, gdy maksimum pierwszego przypada nie bli¿ej ni¿ na pierwsze minimum drugiego. Na rysunku pokazano prą¿ki g³ówne otrzymane przy u¿yciu siatki o 10 rysach (N = 10).
Na rys. 49 pokazano rozk³ad natê¿eñ dla którego, zgodnie z tzw kryterium Rayleigha, mo¿na jeszcze rozró¿niæ dwie bliskie d³ugości fali, l 1 i l 2. Kryterium to jest oczywiście trochê arbitralne, ale jest to w tej sytuacji nieuniknione. Poniewa¿ pierwsze minimum dla d³ugości fali l wypada dla d = m + 1/N, otrzymujemy:

Kąt a
1 odpowiada maksimum (d
= m) dla d³ugości fali l
1, natomiast kąt a
2 odpowiada maksimum dla d³ugości fali l
2, ale jednocześnie bêdzie to, zgodnie z kryterium Rayleigha, minimum dla d³ugości fali l
1. Oznaczmy ![]() literą F
. Mamy wówczas:
literą F
. Mamy wówczas:
![]() ,
,
z drugiej zaś strony, z poprzedniego wzoru:
![]() ,
,
czyli
![]() ,
,
zatem, zestawiając dwa odpowiednie wzory razem otrzymujemy ostatecznie:
![]()
gdzie  określa siê mianem zdolności rozdzielczej.

Rys. 50. Dziêki zastosowaniu soczewek mo¿liwe jest spe³nienie warunku Fraunhofera w niewielkiej objêtości. P³aszczyzny szczeliny wejściowej (S) i wyjściowej (P) są p³aszczyznami ogniskowymi dwóch soczewek. Dziêki temu wiązki świat³a przechodzące przez ekran z otworami są równoleg³e, pomimo, i¿ odleg³ości punktów S i P od ekranu są stosunkowo niewielkie.
Stosowanie dyfrakcji i interferencji Fraunhofera do analizy dzia³ania przyrządów optycznych, których wymiary z pewnością nie są tak du¿e jak wymaga³by tego warunek Fraunhofera, wymaga jednak pewnego uzasadnienia. Spe³nienie warunku Fraunhofera jest mo¿liwe dziêki zastosowaniu uk³adów optycznych, tak jak pokazuje to rys. 50. Mogą to byæ soczewki, chocia¿ czêściej równoleg³ośæ wiązki świat³a padającego na siatkê dyfrakcyjną zapewnia zwierciad³o, w którego ognisku znajduje siê szczelina wejściowa. Równoleg³a wiązka ugiêta na siatce jest zbierana przez nastêpne zwierciad³o i skupiana na szczelinie wyjściowej znajdującej siê w p³aszczynie ogniskowej tego zwierciad³a (punkt P). Ka¿dej d³ugości fali odpowiadaæ bêdzie inna wiązka, rozchodząca siê pod odpowiednio ró¿nym kątem; tak wiêc tylko jedna z nich o d³ugości fali odpowiadającej danemu kątowi a obrotu siatki, zostanie zogniskowana na szczelinie wyjściowej i mo¿e opuściæ uk³ad. Taka w³aśnie jest zasada dzia³ania spektrometru opartego na siatce dyfrakcyjnej.
Prostokątny uk³ad otworów
Nastêpny uk³ad, który rozpatrzymy to prostokątny uk³ad jednakowych otworów, pokazany na rys. 44. Przyjmijmy, ¿e uk³ad ten ma N kolumn i M wierszy.
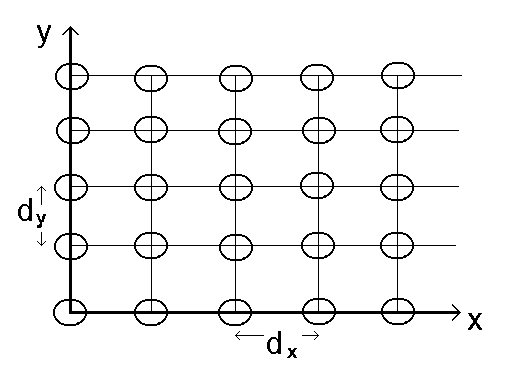
Rys. 51. Prostokątny uk³ad jednakowych otworów. Odleg³ośæ pomiêdzy kolejnymi otworami w kierunku y wynosi dy, a w kierunku x, dx.
Po³o¿enie otworu le¿ącego w j-tej kolumnie i l-tym wierszu mo¿e byæ opisane nastêpującymi wspó³rzêdnymi w uk³adzie Oxy:
![]() .
.
Przyjmując, ¿e:
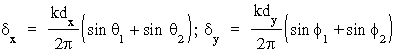 ,
,
otrzymamy nastêpujące wyra¿enie na czynnik interferencyjny F:
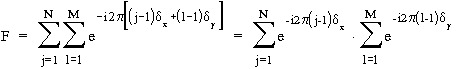 .
.
Wyra¿enie to ma postaæ iloczynu dwóch czêści, które mają postaæ analogiczną do tej, którą otrzymaliśmy wcześniej dla siatki dyfrakcyjnej (mo¿na by³oby powiedzieæ, ¿e rozpatrywany obecnie uk³ad to dwuwymiarowa siatka dyfrakcyjna). Postêpując podobnie jak poprzednio otrzymamy zatem:
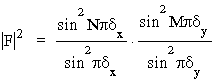 ,
,
rozwiązanie, które jest znowu iloczynem dwóch cz³onów o znajomej postaci.
Jak pamiêtamy, dla siatki dyfrakcyjnej punkty w przestrzeni charakteryzujące siê jednakowym natê¿eniem le¿a³y na sto¿kach, opisanych równaniem q
2 = const. Równanie to bierze siê z warunku ![]() = const, uzupe³nionym o warunek sta³ego po³o¿enia ród³a, q
1 = const. Wierzcho³ki tych sto¿ków (z których ka¿dy odpowiada innej wartości d
, a wiêc innej wartości natê¿enia świat³a) le¿ą w punkcie O, oś obrotu jest osią Ox, a tworzące to wektory po³o¿enia ró¿nych punktów P, R20. Oczywiście dla dwymiarowego przypadku sytuacja siê skomplikuje; zbiór punktów w przestrzeni odpowiadający sta³emu natê¿eniu musi charakteryzowaæ siê sta³ym d
x i d
y, zatem musimy wziąæ pod uwagê dwie rodziny sto¿ków; oprócz sto¿ków q
2 = const, mamy tak¿e sto¿ki f
2 = const. Ta druga rodzina sto¿ków bêdzie mia³a wspólny wierzcho³ek w punkcie O i wspólną oś obrotu Oy. Ich przeciêcia z ekranem równoleg³ym do p³aszczyzny Oxy to bêdą hiperbole o osiach prostopad³ych do hiperbol q
2 = const; z kolei przeciêcia obu rodzin hiperbol wyznaczą punkty na ekranie, dla których natê¿enie świat³a bêdzie mia³o wartośæ równą iloczynowi wartości odpowiadających ka¿dej z przecinających siê hiperbol.
= const, uzupe³nionym o warunek sta³ego po³o¿enia ród³a, q
1 = const. Wierzcho³ki tych sto¿ków (z których ka¿dy odpowiada innej wartości d
, a wiêc innej wartości natê¿enia świat³a) le¿ą w punkcie O, oś obrotu jest osią Ox, a tworzące to wektory po³o¿enia ró¿nych punktów P, R20. Oczywiście dla dwymiarowego przypadku sytuacja siê skomplikuje; zbiór punktów w przestrzeni odpowiadający sta³emu natê¿eniu musi charakteryzowaæ siê sta³ym d
x i d
y, zatem musimy wziąæ pod uwagê dwie rodziny sto¿ków; oprócz sto¿ków q
2 = const, mamy tak¿e sto¿ki f
2 = const. Ta druga rodzina sto¿ków bêdzie mia³a wspólny wierzcho³ek w punkcie O i wspólną oś obrotu Oy. Ich przeciêcia z ekranem równoleg³ym do p³aszczyzny Oxy to bêdą hiperbole o osiach prostopad³ych do hiperbol q
2 = const; z kolei przeciêcia obu rodzin hiperbol wyznaczą punkty na ekranie, dla których natê¿enie świat³a bêdzie mia³o wartośæ równą iloczynowi wartości odpowiadających ka¿dej z przecinających siê hiperbol.
Mo¿na by³oby siê zastanawiaæ, jak bêdzie wygląda³a ca³a ta historia dla trójwymiarowej siatki dyfrakcyjnej. Nale¿y jednak oczekiwaæ, ¿e w wyniku przeciêcia trzech rodzin sto¿ków otrzymalibśmy zbiór pojedynczych punktów w przestrzeni. Tymczasem dla siatki jednowymiarowej mieliśmy powierzchniê, a dla siatki dwuwymiarowej krzywą, które na ekranie dadzą w pierwszym wypadku krzywe, a w drugim przypadku punkty. Trzeba raczej przypadku, ¿eby przeciêcie ekranem zbioru punktów w przestrzeni da³o cokolwiek sensownego. Przypadek trójwymiarowy nie wnosi zatem nic specjalnego do dziedziny, w której ekran odgrywa rolê tak wa¿ną jak w³aśnie w optyce. Jednak spotkacie siê z podobnym zagadnieniem tylko nie w optyce ale w fizyce cia³a sta³ego...