,WYK£AD 12
2.5 Odbicie i za³amanie świat³a na granicy dwóch ośrodków
Rozwiązania równañ Maxwella na granicy dwóch ośrodków; warunki graniczne
Rozpatrywane przez nas do tej pory ośrodki materialne by³y zawsze jednorodne; tzn ich w³asności nie zmienia³y siê od punktu do punktu. Oznacza³o to, ¿e parametry makroskopowe charakteryzujące ośrodek, takie jak przenikalnośæ elektryczna czy magnetyczna, nie by³y zale¿ne od wspó³rzêdnych przestrzennych. Granica pomiêdzy dwoma ośrodkami jednorodnymi, gdzie w³asności te zmieniają siê skokowo, stanowi wa¿ny przyk³ad jakościowo zupe³nie innej sytuacji, którą warto rozwa¿yæ bardziej szczegó³owo. Zaczniemy od sformu³owania tzw warunków granicznych (czasami nazywanymi warunkami brzegowymi), których spe³nienie przez pola elektryczne i magnetyczne jednocześnie w obu ośrodkach, po obu stronach p³aszczyzny rozdzielającej te ośrodki, jest narzucone przez równania Maxwella. Przekonamy siê, ¿e warunki te prowadzą do rozwiązañ dla fali odbitej i za³amanej zgodnych z wcześniej ju¿ przez nas poznanymi prawami; prawem odbicia i za³amania świat³a na granicy pomiêdzy dwoma ośrodkami. Otrzymamy tak¿e tzw wzory Fresnela, które pozwolą nam otrzymaæ relacje pomiêdzy amplitudami fali padającej, odbitej i za³amanej.
Niech p³aszczyzna graniczna rozdziela dwa ró¿ne, ale jednorodne, izotropowe i nieprzewodzące ośrodki materialne. W naszych rozwa¿aniach wykorzystamy równania Maxwella i twierdzenia Gaussa oraz Stokesa. Przypominamy zatem twierdzenie Gaussa:
,
ca³ka z dywergencji pewnego wektora A po objêtości V jest równa ca³ce ze sk³adowej normalnej tego wektora po powierzchni ograniczającej objêtośæ Gaussa V. Natomiast twierdzenie Stokesa mówi, ¿e:
ca³ka po powierzchni S z rotacji pewnego wektora A jest równa ca³ce po krzywej Stokesa G ograniczającej powierzchniê S, ze sk³adowej stycznej wektora A. Oczywiście wykorzystaæ nale¿y odpowiednie równania Maxwella; kluczową sprawą bêdzie tak¿e w³aściwy dobór objêtości V i krzywej G , tak jak pokazano na rysunkach 35 i 36.
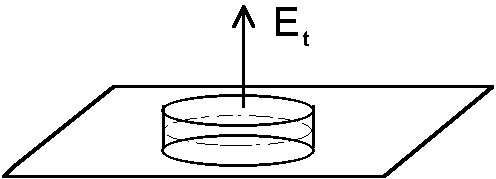
Rys. 35. P³aszczyzna graniczna pomiêdzy dwoma ośrodkami. Cylindryczna zamkniêta powierzchnia Gaussa V obejmuje bardzo ma³y fragment p³aszczyzny granicznej. Pokazana jest sk³adowa Et pola elektrycznego E prostopad³a do powierzchni granicznej, po jednej stronie granicy pomiêdzy ośrodkami.
Rys. 36. P³aszczyzna graniczna pomiêdzy dwoma ośrodkami. Prostokątna zamkniêta krzywa Stokesa G przecina powierzchniê graniczną. Pokazana jest sk³adowa Es pola elektrycznego styczna do powierzchni granicznej.
Poniewa¿:
,
(w ośrodku nieprzewodzącym nie ma ³adunków swobodnych), zatem, wykorzystując twierdzenie Stokesa dla bardzo ma³ej objêtości V otrzymamy:
gdzie indeksy 1 i 2 oznaczają prostopad³e do powierzchni rozdzia³u sk³adowe pola E i P odpowiednio w ośrodku 1 i 2. Przyjêliśmy, ¿e obie powierzchnie D S po obu stronach powierzchni granicznej, stanowiące podstawy walcowej objêtości Gaussa są na tyle ma³e, ¿e wartości wektorów E i P na tych powierzchniach są praktycznie sta³e, a tak¿e, ¿e są one na tyle blisko siebie, i¿ mo¿na pominąæ ca³kê po powierzchni bocznej walca. Mamy zatem pierwszy warunek graniczny:
,
który stwierdza, ¿e sk³adowa prostopad³a wektora D nie zmienia siê na granicy (albo, ¿e zmiana sk³adowej prostopad³ej wektora E jest równa, ze znakiem minus, podzielonej przez e 0 zmianie prostopad³ej sk³adowej wektora polaryzacji P, czyli podzielonej przez e 0 gêstości ³adunku polaryzacyjnego wygenerowanego na powierzchni granicznej).
Z kolei z równania:
po zastosowaniu twierdzenia Stokesa otrzymamy:
gdzie ca³ka powierzchniowa po prawej stronie, o ile powierzchnia wydzielona przez zamkniêtą krzywą G jest odpowiednio ma³a, jest równa w przybli¿eniu zero.
Zatem nastêpny warunek graniczny, dla sk³adowych stycznych pola elektrycznego bêdzie:
,
sk³adowe styczne pola elektrycznego E po obu stronach powierzchni granicznej są sobie równe.
Poniewa¿ podobne rozumowanie mo¿na tak¿e zastosowaæ do pola magnetycznego B otrzymamy, dla ośrodka niemagnetycznego:
poniewa¿ w ośrodku takim nie ma namagnesowania, które odpowiada³oby polaryzacji w dielektryku. Powy¿sze równanie wynik³o z równania divB =0. Z kolei z równania c2rotB = ¶ E/¶ t, wykorzystując twierdzenie Stokesa i odpowiedni wybór pêtli G , analogicznie jak dla pola E, otrzymamy:
Pole magnetyczne B jest zatem ciąg³e na granicy pomiêdzy dwoma ośrodkami niemagnetycznymi, dla których, na tej¿e granicy, nie ma namagnesowania M (a wiêc i jego skoku).
Warto zwróciæ uwagê, ¿e warunki graniczne mo¿na sformu³owaæ wprost, analizując równania Maxwella (zainteresowanych odsy³amy do Feynmana, t. 2, cz. 2, podrozdzia³ 33-3), a tak¿e, ¿e tylko jeden z tych warunków, o sk³adowej pola E normalnej do powierzchni granicznej, zosta³ sformu³owany przy za³o¿eniu, ¿e gêstośæ ³adunków swobodnych jest zero (ośrodki nieprzewodzące). O ile zatem uda nam siê uniknąæ u¿ycia tego warunku (spróbujemy tego dokonaæ), wyprowadzone przez nas wzory powinny byæ s³uszne ogólnie, tak¿e dla ośrodków przewodzących.
Fala padająca, odbita i za³amana
Jak pamiêtamy z poprzednich wyk³adów, harmoniczna fala p³aska rozchodząca siê w ośrodku izotropowym mo¿e byæ przedstawiona w nastêpujący sposób:
; 
,
gdzie k jest wektorem falowym w ośrodku materialnym, którego urojona czêśæ, dla zespolonego wspó³czynnika za³amania charakteryzującego dany ośrodek nz, bêdzie zawieraæ wektor ekstynkcji a opisujący zmianê amplitudy fali z odleg³ością. Oczywiście wektor k0 to wektor falowy danej fali w pró¿ni. Podane wy¿ej wyra¿enie opisujące wektor B mo¿na otrzymaæ ³atwo z równania Faradaya:
zastêpując sk³adowe operatora Ñ sk³adowymi wektora ik, a ró¿niczkowanie po czasie mno¿eniem przez -iw . Otrzymamy wtedy
.
A zatem falê padającą, odbitą i za³amaną, pokazane na rysunku 37, mo¿emy zapisaæ w nastêpujący sposób:
; 
; 
; 
; 
,
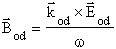gdzie za³o¿yliśmy, ¿e wszystkie fale, na które sk³adają siê fala pierwotna (padająca) i fale wtórne wygenerowane w ośrodku, charakteryzują siê tą samą czêstością w .
Rys. 37. Fala rozchodząca siê w ośrodku o wspó³czynniku za³amania n1 pada na powierzchniê oddzielającą ośrodek 1 od ośrodka 2 (wspó³czynnik za³amania n2) wytwarzając falê odbitą i za³amaną.
Zauwa¿my, ¿e ze wzglêdu na wybór osi uk³adu wspó³rzêdnych wektory falowe wszystkich trzech fal bêdą mia³y tylko sk³adowe x i z, gdy¿ tylko te sk³adowe le¿ą w p³aszczy¼nie padania xz. Co wiêcej, jeśli wybierzemy polaryzacjê fali padającej w taki sposób, by wektor E mia³ ró¿ną od zera tylko sk³adową y (Ey ¹ 0, Ex = Ez = 0) to pole E nie ma sk³adowej prostopad³ej do powierzchni rozdzia³u i pierwszy warunek graniczny nie bêdzie nam potrzebny (wiemy i tak, ¿e sk³adowe prostopad³e pól E, P są równe zero ze wzglêdu na szczególny wybór polaryzacji fali padającej).
Uwzglêdniając zatem, ¿e ca³kowite pole E w ośrodku 1 sk³ada siê z fali padającej i odbitej, a w ośrodku 2 z fali za³amanej, warunek ciąg³ości sk³adowej stycznej na granicy ośrodków (zatem dla z = 0) dla polaryzacji prostopad³ej do p³aszczyzny padania, da nam nastêpujące równanie:
,
które musi byæ spe³nione dla ka¿dego x i oczywiście dla ka¿dego t.
Biorąc t = 0 otrzymamy:
.
Poniewa¿ jest to równanie, w którym wystêpują oscylujące funkcje okresowe, spe³nienie tego równania wymaga, by okresy oscylacji by³y jednakowe (o ile amplitudy nie są równe zero), zatem:
sk³adowe x wektorów falowych wszystkich trzech fal muszą byæ sobie równe no i
otrzymaliśmy pewną relacjê dla amplitud, którą wykorzystamy pó¼niej.
Prawo odbicia i prawo Snella
Poniewa¿, w rozwa¿anym przez nas przypadku, obie fale w ośrodku 1, tzn fala padająca i odbita, rozchodzą siê w tym samym ośrodku, zatem dlugości wektorów falowych dla tych fal, zale¿ne od wspó³czynników za³amania (k = k0n) tak¿e muszą byæ jednakowe, czyli:
,
co, wobec równości sk³adowych x prowadzi do wniosku, ¿e:
czyli 
lub 
Pierwsze z tych rozwiązañ nie ma sensu (bo to nie jest w ogóle fala odbita), a z drugiego wynika, ¿e kąt padania i kąt odbicia muszą byæ sobie równe! Tak wiêc uda³o nam siê udowodniæ prawo odbicia świat³a.
Rozpatrzymy teraz wektory falowe fali padającej i za³amanej. Mamy oczywiście:
,
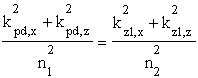gdy¿ wspó³czynniki za³amania nie są ju¿ równe zatem i d³ugości wektorów falowych nie bêdą równe. Wobec równości sk³adowych x mo¿na u¿yæ powy¼szego równania do znalezienia wartości sk³adowej z wektora falowego fali za³amanej w zale¿ności od sk³adowych wektora falowego fali padającej. Powrócimy do tego za chwilê, gdy¿ równanie to ma ciekawsze konsekwencje, którymi zajmiemy siê teraz. W specjalnym przypadku, gdy wektory kpd i kod są rzeczywiste, to:
, a tak¿e 
Stosunek sinusów, wobec równości sk³adowych x bêdzie zatem równy stosunkowi d³ugości obu wektorów falowych, który z kolei jest przecie¿ równy stosunkowi wspó³czynników za³amania. Mamy zatem:
czyli otrzymaliśmy prawo Snella.
Wzory Fresnela, padanie i odbicie normalne
Powrócimy teraz do ogólnego przypadku, dla którego wspó³czynniki za³amania obu ośrodków mogą byæ zespolone. Warto zauwa¿yæ, ¿e jak na razie nie korzystaliśmy z warunku dla sk³adowych normalnych wiêc wzory nasze, z wyjątkiem prawa Snella, są dobre nawet dla ośrodków przewodzących (jak chodzi o prawo Snella, to wspó³czynniki za³amania powinny byæ rzeczywiste, czyli nie tylko ośrodki muszą byæ nieprzewodzące, ale musimy byæ tak¿e daleko od rezonansu, ¿eby t³umienie w ośrodku nie wprowadzi³o czêści urojonej do sta³ej dielektrycznej). By³oby postêpem (prawo odbicia i prawo Snella przecie¿ ju¿ poznaliśmy wcześniej), gdybyśmy potrafili powiedzieæ coś wiecej o amplitudach fal odbitej i za³amanej. Jedna relacja, którą znale¼liśmy wy¿ej:
,
nie wystarcza, mamy bowiem jedno równanie i dwie niewiadome, E0 i E0 (chcemy wyraziæ amplitudy E0 i E0 przez amplitudê E0, która, wobec tego, nie jest niewiadomą). Potrzebujemy zatem jeszcze jednego równania wią¿ącego ze sobą wszystkie trzy amplitudy. Mo¿na ³atwo sprawdziæ, ¿e równania takiego dostarczy warunek ciąg³ości sk³adowej stycznej do powierzchni granicznej pola magnetycznego B (warunek ciąg³ości sk³adowych normalnych da to samo równanie, nic nowego i niezale¿nego). Poniewa¿ pole B = k´ E/w , a w rozwa¿anym przez nas przypadku pole E jest skierowane prostopadle do p³aszczyzny padania (Ey ¹ 0, Ex = Ez = 0), zatem sk³adowa styczna do powierzchni granicznej pola B bêdzie sk³adową x. Mamy zatem:
czyli 
Z równania tego, po podstawieniu wyra¿eñ na fale padającą, odbitą i za³amaną, otrzymamy:
.
Dla z = 0 i t = 0, biorąc pod uwagê, tak jak poprzednio, ¿e równanie to musi byæ spe³nione dla wszystkich x, otrzymamy nastêpujące wyra¿enie, wią¿ące ze sobą amplitudy trzech fal:
Poniewa¿ wcześniej pokazaliśmy, ¿e
, mamy nastêpujący uk³ad dwóch równañ:
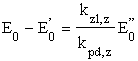i 
,
skąd mo¿na ³atwo otrzymaæ nastêpujące związki pomiêdzy amplitudami trzech fal:
oraz 
Ostatecznie mamy: 
i 
.
Chocia¿ wzory te wyglądają na dośæ skomplikowane, bardzo ³atwo mo¿na z nich wywnioskowaæ relacje pomiêdzy amplitudami trzech fal dla padania normalnego. Oczywiście dla padania normalnego d³ugości sk³adowych z wektorów falowych są po prostu równe d³ugościom samych wektorów falowych (skladowe x są równe zero) i, biorąc pod uwagê, ¿e kpd = k0n1 i ¿e kxl = k0n2, mamy:
i 
.
Wyra¿enia te na dodatek nie są zale¿ne od polaryzacji, bo dla padania normalnego i ośrodków izotropowych obie polaryzacje są ca³kowicie równowa¿ne. Poniewa¿ natê¿enie fali wyra¿a siê poprzez wektor Poyntinga, jest ono zatem proporcjonalne do iloczynu pola elektrycznego i magnetycznego; z kolei wartośæ pola magnetycznego wyra¿a siê poprzez iloczyn pola elektrycznego i wspó³czynnika za³amania. Mamy zatem:
, 
, a tak¿e 
i, ostatecznie:
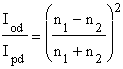oraz 
.
£atwo tak¿e sprawdziæ, ¿e:
,
czego nale¿a³o oczekiwaæ.
Wracając do wzoru dla dowolnego kąta padania, poniewa¿:
, oraz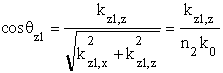 
mamy zatem:
.
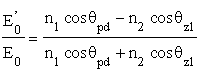Wykorzystamy teraz prawo Snella i wyeliminujemy wspó³czynniki za³amania podstawiając za n2 odpowiednie wyra¿enie,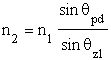 
. Wspó³czynnik za³amania n1 skróci siê i otrzymamy nastêpujący wzór na stosunek amplitud fali za³amanej i padającej dla rozpatrywanej polaryzacji:
, polaryzacja równoleg³a.
Nieco bardziej ¿mudne, choæ podobne rachunki dla drugiej polaryzacji, dla której wektor elektryczny jest prostopad³y do p³aszczyzny padania prowadzą do nastêpującego wzoru:
, polaryzacja prostopad³a do p³aszczyzny padania.
Wzory na wspó³czynniki odbicia dla obu polaryzacji:
, oraz 
noszą nazwê wzorów Fresnela. (Prawdopodobnie wiêkszośæ z Was zauwa¿y³a, ¿e wyprowadzenie to w rzeczywistości jest poprawne tylko dla rzeczywistych wspó³czynników za³amania....)
Kąt Brewstera i ca³kowite wewnêtrzne odbicie
Analiza wzorów Fresnela wskazuje, ¿e dla przypadku, gdy q pd + q zl = 90° jeden ze wspó³czynników odbicia, Rrown = 0. Zatem dla pewnego kąta padania, dla którego bêdzie spe³niony warunek q pd + q zl = 90° , fala odbita bêdzie ca³kowicie spolaryzowana liniowo. Kąt taki nazywamy kątem Brewstera.
Inny ciekawy przypadek zachodzi gdy n1 > n2, tzn fala pada ze strony ośrodka gêstszego. Gdy kąt padania bêdzie wiêkszy od pewnej wartości krytycznej, dla której kąt za³amania staje siê równy 90° :
,
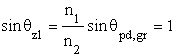mamy problem, oznacza to bowiem, ¿e poniewa¿ dalszy wzrost kąta padania nie mo¿e byæ ju¿ kompensowany wzrostem kąta za³amania, powstaje pytanie, co z prawem Snella, co siê bêdzie dla takich wiêkszych kątów dzia³o.
Obliczmy sk³adową z wektora falowego fali za³amanej:
,
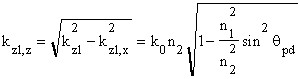gdzie wykorzystaliśmy udowodniony wcześniej fakt, ¿e sk³adowe x wektora falowego fali za³amanej i padającej są równe (tak¿e odbitej, choæ to nie jest teraz potrzebne). Je¿eli kąt padania jest wiêkszy od kąta granicznego, wyra¿enie pod pierwiastkiem jest ujemne i sk³adowa z wektora falowego fali za³amanej jest w takim razie urojona. To zaś oznacza, ¿e rozwiązanie przedstawiające falê za³amaną bêdzie mia³o postaæ:
gdzie
.
A zatem fala za³amana bêdzie t³umiona w kierunku osi z czyli w g³ąb ośrodka, t³umiona tym silniej, im bardziej kąt padania bêdzie wiêkszy od kąta granicznego. Oczywiście te komplikacje nie dotyczą fali odbitej, która bêdzie opisana tak jak zawsze, wyra¿eniem bez t³umienia. Problem prawa Snella zatem siê rozwiązuje w nastêpujący najprostszy mo¿liwy sposób: znika fala za³amana i razem z nią tak¿e samo prawo Snella.