Złote zderzenia

Grzegorz Karwasz, Andrzej Karbowski

Zakład Dydaktyki Fizyki, Instytut Fizyki UMK w Toruniu

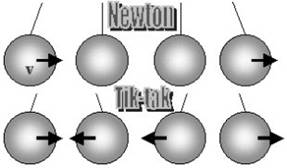
Wahadło Newtona [1], riki-tiki [2], spadające piłeczki [3] z wystaw "Fizyki zabawek" to kolejne przybliżenia problemu zderzeń centralnych dwóch punktów materialnych. W obecnej pracy rozszerzamy zabawę na zderzenia wózków (o różnych masach) na szynie (lub torze powietrznym). W szczególnie zabawnym przypadku stosunki mas przypominają regułę złotego podziału.

Rys. 1. Wahadło Newtona.	Rys. 2. Riki-tiki	Rys. 3. Skaczące piłeczki.

Praca "Toys and Physics" (i jej polska wersja [1-3]) to niezwykle krótki (6-zdaniowy na dane zagadnienie) podręcznik fizyki. Krótki dlatego, aby utrzymać uwagę internetowego czytelnika do końca zagadnienia. Niestety, lakoniczność opisów nie pozwala na klarowne pokazanie ścieżek dydaktycznych.

W dziale mechanika, zderzenia centralne są drugim tematem poruszanym, po zagadnieniu równowagi statycznej. Zaczynamy od wahadła Newtona, w którym w nieruchomą kulkę uderza inna, o tej samej masie (patrz Rys. 4). Wbrew pozorom, rozwiązanie nie jest tak do końca "lakoniczne", jak to opisujemy na stronie [1], a wymaga nieco dokładniejszej analizy [4]. Obrazowo możemy jednak powiedzieć, że kulki "wymieniają się pędami".

Zderzenia tik-taka są inne, a mianowicie obie kulki mają tę samą prędkość i obie odskakują (choć możliwe jest też zderzenie jak w wahadle Newtona, tzn. jedna kulka spada, a druga początkowo spoczywa). I w tym przypadku możemy mówić o "wymianie pędu".

Rys. 4. Wahadło Newtona u góry oraz tik-tak poniżej.

Zepsuta zabawka tik-tak, z jedną częściowo rozbitą kulką daje nam nowe możliwości badań zderzeń ciał o różnych masach. Kulka o większej masie uderza z pewną prędkością w spoczywającą kulkę o mniejszej masie i ta odskakuje z większą prędkością.

Rozwiązanie skaczących piłeczek jest jeszcze trudniejsze – wymaga założenia o nieskończoności stosunku masy piłki cięższej do lekkiej. Wówczas wysokość na jaką wzniesie się lżejsza piłeczka po odbiciu jest dziewięciokrotnie większa niż dla piłeczki cięższej.

I w końcu "dropper popper", to zderzenia supersprężyste, w którym zysk energii pochodzi nie ze zderzenia, ale z energii sprężystości. Podobnie zresztą jak w naszej wersji działa magnetycznego na wystawie pt. "Z górki na pazurki" [5].

Komputerowy system pomiarowy z długą szyną np. firmy Pasco lub tor powietrzny Pana Tabaszewskiego pozwalają na wykonanie ciekawych doświadczeń z kinematyki i dynamiki. Można np. sprawdzić jakie muszą być masy wózków, aby zaszło podwójne zderzenie.

Jak wiemy, gdy cięższy obiekt uderza w lżejszy np. słoń w muchę, to cięższy traci tylko część prędkości opisaną oczywiście równaniami zasad zachowania pędu i energii.

Szyna pomiarowa zestawu PASCO lub tor powietrzny z wózkami o łatwo zmienianej masie daje nam kolejne możliwości eksperymentowania np. takiego zderzenia dwóch wózków, w którym uderzający wózek zatrzymuje się, ale dopiero po drugim zderzeniu [6]. Oczywiście masa pierwszego wózka A musi być większa niż drugiego B, ale o ile?

Poniższe rysunki (5, 6, 7 i 8) przedstawiają schemat doświadczenia.

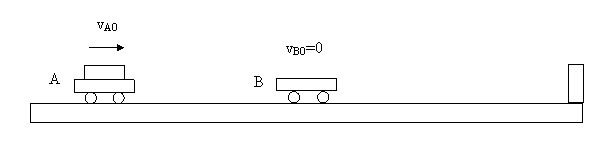
Rys. 5. Wózek A porusza się w prawo po poziomym torze i uderza w spoczywający wózek B.

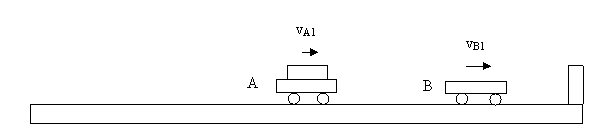
Rys. 6. Wózek A zderzył się z wózkiem B i w wyniku tego jeden i drugi poruszają się w prawo po poziomym torze.

Rys. 7. Wózek B odbił się od zderzaka Z przymocowanego do toru i porusza się w lewo, wózek A cały czas porusza się w prawo po torze.

Rys. 8. Wózki A i B zderzyły się ponownie na torze. Wózek A zatrzymał się, natomiast wózek B porusza się w prawo.

Po wykonaniu obliczeń w rozwiązaniu , pojawia się podobnie jak w zagadnieniu złotego podziału , gdzie j oznacza złotą liczbę (»1,6180), stąd tytuł artykułu.

Trzy uwagi – pierwsza dydaktyczna. W nowej podstawie programowej dla gimnazjum nie ma zasady zachowania pędu, co nas jednak nie zwalnia z jej stosowalności.

Druga historyczna – trzy prawa mechaniki Newtona są poprawioną wersją trzech praw Kartezjusza. Dwa pierwsze są w zasadzie identyczne, a w trzecim Kartezjusz mówił nie o równoważnych siłach, ale o wymianie pędu: "z dwóch zderzających się ciał jedno zyskuje tyle pędu, ile drugie traci". Trzecia metodyczna – we wszystkich opisanych doświadczeniach, a w szczególności w wahadle Newtona zderzenia muszą być "jednowymiarowe", tzn. centralne. W przeciwnym razie wahadło Newtona "nie działa", ale to już inna historia.

Literatura:

[1] A. Kamińska, G. Karwasz, Wahadło Newtona, w "Physics and Toys", praca zbiorowa pod
red. G. Karwasza, Pomorska Akademia Pedagogiczna, 2006,

http://dydaktyka.fizyka.umk.pl/zabawki1/files/mech/wahnewt-pl.html

[2] http://dydaktyka.fizyka.umk.pl/zabawki1/files/mech/rikitiki-pl.html

[3] skaczące piłeczki (spadające piłeczki)
http://dydaktyka.fizyka.umk.pl/zabawki1/files/mech/pileczki-pl.html

[4] A. Kamińska, G. Karwasz, Wahadło Newtona, j.w.

http://dydaktyka.fizyka.umk.pl/zabawki1/files/mech/wahnewt_big-pl.html

[5] G. Karwasz, G. Osiński, K. Służewski, A. Karbowski, W. Krychowiak

http://dydaktyka.fizyka.umk.pl/pazurki/galileo.html

[6] http://www.fizyka.umk.pl/~akarb/Zlote_zderzenia_pliki/Zderzenia.wmv