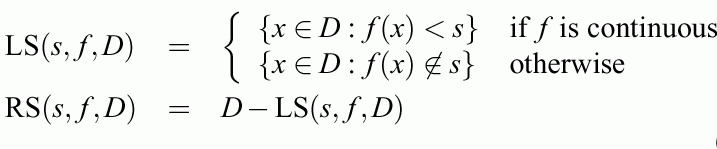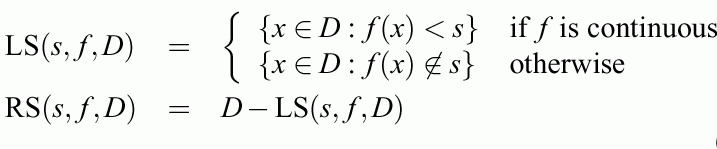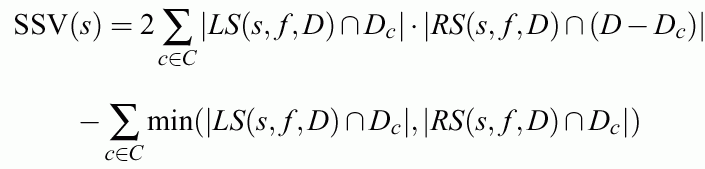SSV, Separability Split Value decision tree
SSV separability criterion: choose the feature for which a split value is found that allows to
- separate maximum number of vector pairs from different classes
- if different splits lead to the same result minimize the number of separated pairs from the same class.
Note: this is a heuristic criterion.
Separability is maximized, not the number of errors system makes.
Define the left set and the right set:
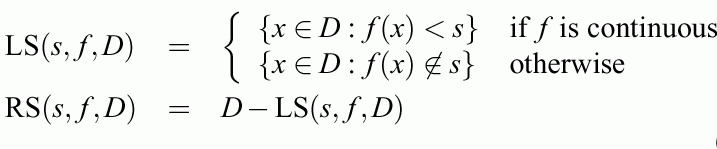
The SSV criterion for the test s counts the no. of elements from class c in the left set and from all other clases in the right set, summing over all classes:
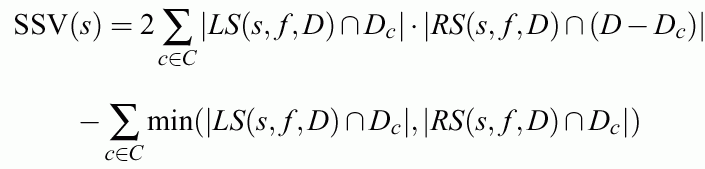
The second term sums the number of cases from the same class; factor 2 is added to ensure that the first term dominates and the second counts only when the first terms are equal.
- Simple criterion;
- automatic - no paramters;
- gives useful linguistic variables;
- deals with symbolic, discrete and continuous features;
- handles missing values - as ?, one of the symbolic values.
Applications: discretization, feature selection, rules, decision trees.
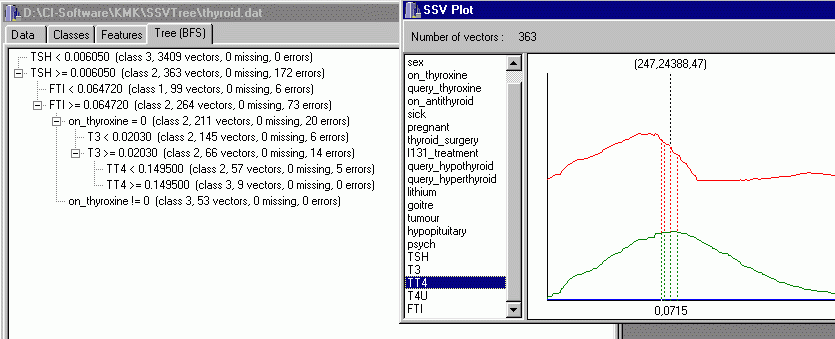
Each node of the tree is described by:
- the split condition
- the number of vectors in the node (satisfying the condition)
- the number of missing values within that vectors for the split feature
- the number of erroneously classified vectors.
The SSV plot shows criterion values against split values for the feature
selected in the list on the left. The plot lines show the following:
- red - the number of errors if we add the split to the tree
- green - the first part of SSV - the number of correctly separated pairs
- blue - the second part of SSV - the number of separated pairs from the same class
Remarks:
- the numbers above the SSV plot lines show the values of the red, green
and blue curves for the best split value for the presented feature
- the value below the plot is the best split value for the presented feature
- SSV estimates separability, so it can significantly differ from the error curve (red line)
Some results from the SSV tree and rules.
Włodzisław Duch