Understanding the data

Decision tree methods of knowledge extraction

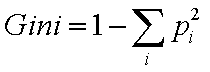
General remarks:
Decision Trees (DT) are simple to use, have a few parameters, provide simple rules.

Most DT are univariate, axis-parallel.
Oblique trees use linear combinations of input features.

D - training set partitioned into D_k subsets by some tests T.
Stop(D_k)=True if assumed leaf purity is reached.

• If Stop(D) the tree is a leaf associated with the most frequent class in D.
• Test T has mutually exclusive outcomes T_i, i =1...K, subset D_i is composed from cases for which T_i=True.
• Splitting criterion is defined S(T(x)).
• For a discrete attribute test A=?
• A<t for a continuous attribute A;
  if A has values v₁< v₂< ... v_N< check all t = (v_i+ v_i+1)/2;
  select the best S(T(t))

Trees are pruned to improve generalization and to generate simpler rules.

CART, Classification and Regression Tree

Breiman, L., Friedman, J., Olshen, R., and Stone, C. (1984) Classification and Regression Trees", Wadsworth.

Split criterion is based on Gini(feature,split) index:

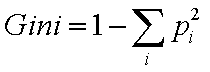
p_i is the probability of class i vectors in the node.
For "pure node" probabilities are binary and Gini=0

For each possible split calculate Gini, select split with minimum impurity.
Use minimal cost-complexity pruning, rather sophisticated.

DB-CART - added boosting and bagging.
Boosting: making a committee of many classifiers trained on the same training data, with re-weighted wrongly classified cases.
Bagging, bootstrap aggregating: making a committee of many classifiers trained on subsets of data created from the training set by bootstrap sampling (i.e. drawing samples with replacement).

Commercial version of CART and IndCART: different ways of handling missing values and pruning.

C 4.5

Quinlan, J. R. (1993). C4.5: Programs for Machine Learning. San Mateo: Morgan Kaufmann.

C 4.5 splitting criterion is the gain ratio:
for C classes and fraction p(D;j)=p(C_j|D) in j-th class
the number of information bits the set D contains is:

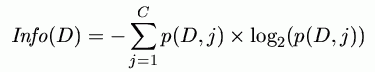
For 2 classes information (vertical) changes with p(D;1)=1-p(D;2) reaching max. for 0.5
Info = expected number of bits required to encode a randomly selected training case.

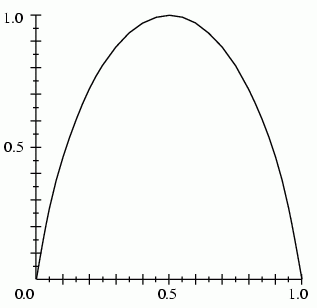
Information gained by a test T with k possible values is:

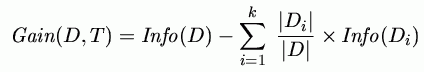
Max. for tests separating D into one-dimensional subsets; attributes with many values are always selected.
Use information gain ratio instead: gain divided by the split information

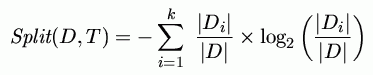
Improvements of continuous attribute treatment in C5:

• The Minimum Description Length (MDL) principle is used: minimize theory and exceptions costs
  Modify Gain(D;T) - log₂ (N-1)/|D|
• Threshold t is chosen to maximize gain.

C4.5 rule generation algorthm, used usually before pruning.
Convert each tree path to a rule:
IF Cond₁ AND Cond₂ ... AND Cond_n THEN class C

• Remove conditions which are not useful.
• Remove empty rules and identical rules.
• Group all rules according to classes.
• Delete rules if the accuracy of the whole set of rules for the class is not lowered.
• Ordered the rules to minimize false positive errors.
• Try to delete rules in turn if accuracy of the whole ruleset on the training set is not lowered.

Z. Zheng, "Scaling Up the Rule Generation of C4.5". Proc. of PAKDD'98, Berlin: Springer Verlag, 348-359, 1998.

Rules are frequently more accurate and simpler than trees, especially if generated from pruned trees.

ANN-DT - Decision Trees from Neural Networks

G.P. J. Schmitz, C. Aldrich, and F.S. Gouws, "ANN-DT: An Algorithm for Extraction of Decision Trees from Artificial Neural Networks". Transactions on Neural Networks 10 (1999) 1392-1401

Train an MLP or RBF model
Generate more data interpolating input points in the neighborhood of the training data (equivalent to adding noise).
Use NN as an oracle to predict class.
Create DT using CART criteria or alternative criteria (correlation between variation of the network and variation of the attribute) to analyze attribute significance.
Prune the network using CART approach.

A few results so far, first good NN should be created.

OC - Oblique Classifier

Many variants of the oblique tree classifiers: CART-LC, CART-AP, OC-1, OC!LP, OC-1AP ...

For some data results are significantly better, trees are smaller, but rules are less comprehensible - combinations of inputs are used.
There is no comparison between neural methods of rule extraction (with aggregation) and oblique trees so far.

Inductive methods

R. Michalski, "A theory and methodology of inductive learning". Artificial Intelligence 20 (1983) 111-161.

StatLog project book:
D. Michie, D.J. Spiegelhalter and C.C. Taylor, "Machine learning, neural and statistical classification". Elis Horwood, London 1994

Many inductive methods have been proposed in machine learning.

PVM

S. Weiss, 1988
Maximize predictive accuracy of a single condition rule, make exhaustive or heuristic search.
Try combinations of 2 conditions.
Expensive but for small datasets finds very simple rules.

RISE - Rule Induction from a Set of Exemplars (Domingos 1996)

Exemplars are maximally specific rules.

• Loop over rules;
• find the nearest example from the same class not yet covered;
• try to generalize existing rule covering the new case - compute change in accuracy and accept it unless classification decreases;
• if no rule is generalized stop.

Use hybrid similarity function, good for nominal and numerical attributes.

Włodzisław Duch